Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.9 - Ex. 23
Encontre uma representação em série de potências para , trace e várias somas parciais na mesma tela. O que acontece quando aumenta?
23.
Passo 1
Pessoal, tudo beleza?
O enunciado quer que a gente represente a função como uma série de potência, faça seu gráfico e suas somas parciais. Também pergunta o que acontece quando aumenta.
Não pira, vamos resolver!
Primeiro vamos tentar achar uma representação de em série de potências:
A divisão de logaritmos pode ser representada dessa forma:
Agora integrando os dois lados, temos:
Essa última integral tem a legítima cara de uma série geométrica, que é o que procuramos quando resolvemos esse tipo de problema.
Passo 2
Podemos escrever essas integrais como séries de potências:
Quando substituímos nesses somatórios por
Onde o primeiro termo é e a razão é , nossa série terá essa cara aqui:
E integrando:
Fazendo-se , descobrimos a constante :
Então,
Passo 3
Show! Agora vamos traçar e várias somas parciais a partir da série de potências encontrada no passo anterior:
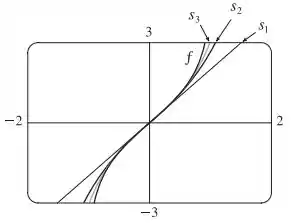
Perceba que, à medida que aumenta, as somas parciais se aproximam cada vez mais de no intervalo de convergência, ou seja, quando .