Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 37
- Encontre a área da região englobada pela parábola e o eixo .
- Encontre o valor de de tal forma que a reta divida a região de (a) em duas regiões de mesma área.
Passo 1
(a)Para encontrar a região englobada por curvas, precisamos analisar a região dada e montar a integral:
Ou
E calculá-la. Vamos lá!
Passo 2
Essa é a nossa região:
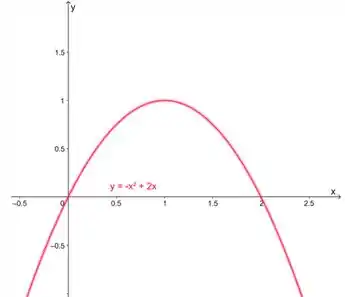
Vemos que ela está limitada superiormente pela parábola e inferiormente pela reta. A gente só precisa calcular:
Os extremos de integração são as raízes da parábola:
Nossa integral fica assim:
Passo 3
Agora é só calcular:
Passo 4
(b) O pulo do gato aqui é perceber que se divide a área da região entre e em duas regiões iguais, podemos dizer que a área entre e é igual a . Vamos lá!
Passo 5
A nossa região tem essa nova carinha:
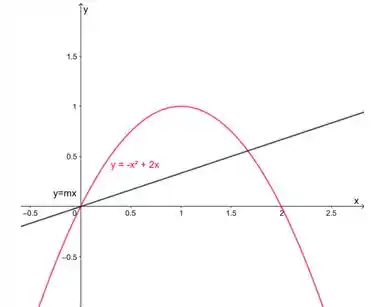
Nossa região é limitada por cima pela parábola e por baixo pela reta.
Para achar os extremos de integração, precisamos da interseção entre os dois gráficos:
A integral, que a gente sabe que dá fica assim:
Passo 6
Agora é só abrir essa integral e substituir o valor de para achar :
Isolando :
Resposta
(a)
(b)