Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 47

Use um gráfico para estimar a intersecção com o eixo x da curva y = 1 - 2 x - 5 x 4 . A seguir, use essa informação para estimar a área da região que se situa sob a curva e acima do eixo x.

Passo 1

O enunciado pede pra que a gente use um gráfico para estimar a intersecção com o eixo x da curva:

y = 1 - 2 x - 5 x 4

Depois a gente deve usar essa informação para estimar a área da região que se situa sob a curva e acima do eixo x.

Através de um software gráfico, temos que o gráfico da função dada é:

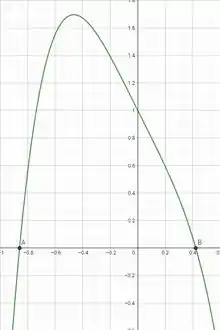
Temos que y = 0 em , x ≈ - 0,86 e x ≈ 0,42 .

Passo 2

Agora é a hora de calcular a área sobre a curva, para isso vamos usar como limite de integração as raízes encontradas no passo 1.

a ≈ - 0,86 e b ≈ 0,42

Assim, a área pedida é dada por:

A = ∫ a b 1 - 2 x - 5 x 4 d x

Passo 3

Sepando os integrandos para melhor visualização temos:

A = ∫ a b d x - 2 ∫ a b x d x - 5 ∫ a b x 4 d x

Integrando temos:

A = b - a - 2 b 2 2 - a 2 2 - 5 b 5 5 - a 5 5 ∴ A = b - a - b 2 - a 2 - b 5 - a 5

Passo 4

Substituindo os valores aproximados de , a e , b temos que

A ≈ 1,36

Resposta

A área aproximada abaixo da curva dada, considerando os extremos a e b é 1,36 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34. Ache a abscissa do centroide da região do exercício 32.
35. Uma partícula move-se ao longo de uma reta de forma que v c m s seja a velocidade da partícula, decorridos ts ; então v = t 2 - t + 1 t + 2 2 ( t 2 + 1 ) ache a fórmula da distância percorrida pel
93. Ache área da região no primeiro quadrante limitada pelo eixo y e pelas curvas y = sec 2 ⁡ xey = t g 2 x .
Ache a área da região limitada pela curva y = e x , pelos eixos x e y e pela reta x = 2 .
Ache a área da região limitada pela curva y = e x e pela reta que passa pelos pontos ( 0 ,1 ) e ( 1 ,e ) .