Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 6
Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da região.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá a seguinte região:
E pede pra a gente esboçar a região delimitada pelas curvas e calcular a sua área utilizando integral. Pra isso a gente tem que decidir se é melhor integrar com relação a ou !
Bora esboçar a área!
Olha, tem funções que de cara já da pra saber o que ela vai ser. Por exemplo, a função , sabemos que ela tem um comportamento especifico sendo positiva em e . Já a função, é uma reta que passa pela origem.
Então, o nosso gráfico vai ser desse jeitinho:
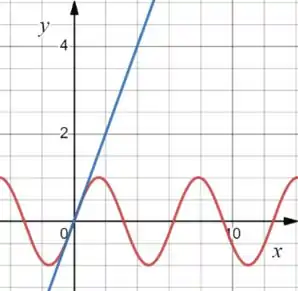
Passo 2
O nosso intervalo vai de até , então o que temos que calcular é essa areazinha de verde:
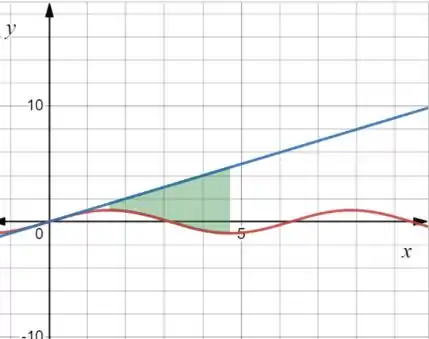
Repara que a curva esta por “cima” e esta por baixo. Se extrairmos uma parte desse retângulo, vamos ter que a altura será a diferença entre as curvas e a largura será a variação de x. Assim:
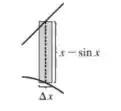
Okay? Agora é só calcularmos a área!! Aqui vai ser mais simples integrar com respeito a !
Passo 3
Montando a integral:
Daí é só calcular a integral normalmente!!
Chegamos em:
Prontinho!