Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.8 - Ex. 1c

1. A - Encontre a solução u x ,   y da equação de Laplace no retângulo 0 < x < a , 0 < y < b , que satisfaz as condições de contorno

u 0 ,   y = 0 ,         u a ,   y = 0 ,             0 < y < b ,

u x , 0 = 0 ,         u x ,   b = g x ,             0 ≤ x ≤ a .

B. Encontre a solução se

g x = x ,           0 ≤ x ≤ a / 2 , a - x ,         a 2 ≤ x ≤ a

C. Para a = 3 e b = 1 , faça o gráfico de u em função de x para diversos valores de y e faça também, o gráfico de u em função de y para diversos valores de x .

D. Faça o gráfico tridimensional de u em função de x e de y . Desenhe, também, diversas curvas de níveis de u x ,   y no plano x y .

Passo 1

L e t r a   C :

Na letra A e na letra B encontramos a solução da nossa Equação de Laplace:

u x , y = ∑ n = 1 ∞ b n s e n n π x a s e n h n π y a    

Onde

b n = 6 - 2 - 1 n + cos ⁡ n π 2   n π   s e n h n π b a

Aqui devemos substituir o a = 3 e o b por 1 :

u x , y = ∑ n = 1 ∞ b n s e n n π x 3 s e n h n π y 3  

Onde...

b n = 6 - 2 - 1 n + cos ⁡ n π 2   n π   s e n h n π 3

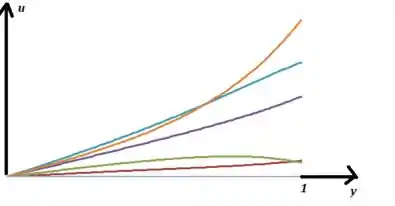
Vamos começar aqui desenhando o gráfico de u em função de x para diversos valores de y . Usando o Excel, podemos desenhar esse gráfico, variando y de 0,2 em 0,2 até chegar 1 e considerando n variando de 1 até 5 (Não há muita necessidade de n muito grande, pois vimos no capítulo que a equação de Laplace converge rapidamente )

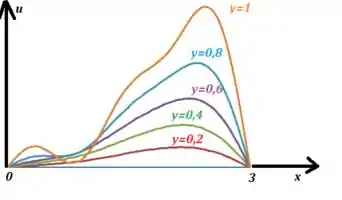
Para o gráfico de u em relação a y , vamos considerar agora o x variando de 0,5 em 0,5 até chegar a 3 :

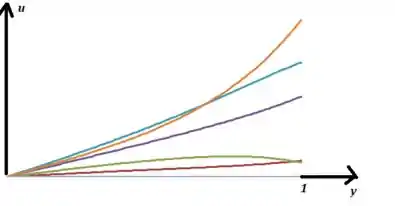
Resposta

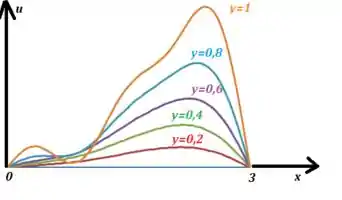
E

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique que a equação diferencial x y ' ' + 1 + 2 n y ' + x y = 0 ,x0 Possui a solução particular y = x - n J n ( x )
Nos problemas 13-18, use os resultados dos problemas 10, 11 e 12 para encontrar uma solução particular para a equação diferencial dada em ( 0 , ∞ ) y ' ' + y = 0
Use a mudança de variável y = x - 1 2 v ( x ) para encontrar a solução geral para a equação x 2 y ' ' + 2 x y ' + λ 2 x 2 y = 0 ,x0
Verifique que a equação diferencial x y ' ' + 1 - 2 n y ' + x y = 0 ,x0 Possui a solução particular y = x n J n ( x )
Nos problemas 13-18, use os resultados dos Problemas 10,11 e 12 para encontrar uma solução particular para a equação diferencial dada em 0 ,∞ . x y ' ' + 3 y ' + x y = 0