Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 38
Encontre todos os pontos de interseção das curvas dadas.
Passo 1
Oie, amigo. Vamos resolver essa atividade agora?
Veja que aqui temos duas curvas:
E queremos encontrar os pontos de intersecção delas.
Para isso basta igualarmos as equações de ambas, e assim iremos encontrar o valor de que satisfaz nossa equação, mas lembre de uma coisa, como cosseno é uma função periódica, iremos encontrar diversos valores.
Passo 2
Vamos começar encontrando os ângulos onde se tem igual:
Lembrando que é o tamanho do vetor em módulo, logo ele pode assumir os valores de e
Dessa forma temos os ângulos de:
Veja que estamos apenas considerando os ângulos da primeira volta, pois a partir da segunda volta em diante, existe uma repetição de valores. Dessa forma temos os seguintes valores de
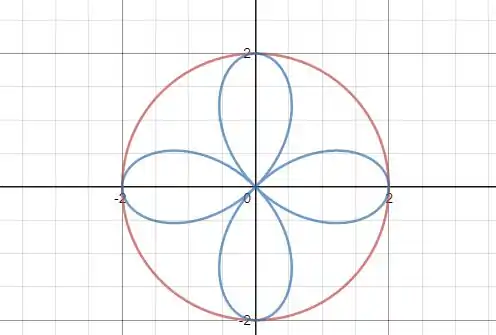
Gráfico das duas curvas para exemplificar o que está acontecendo:
