Encontre todos os pontos de interseção das curvas dadas.
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Aqui a gente quer encontrar todos os pontos de interseção entre as curvas:
E
Quando a gente precisar encontrar esses pontos, a gente deve igualar as equações das curvas para sabermos em quais valores de elas se encontram.
Passo 2
Agora vamos igualar os .
Temos então que o cosseno com esse valor é:
Precisamos saber qual o valor de para esse ângulo, substituindo em qualquer uma das equações:
Esses pontos com certeza terão representações diferentes para as funções, mas de forma polar é assim.
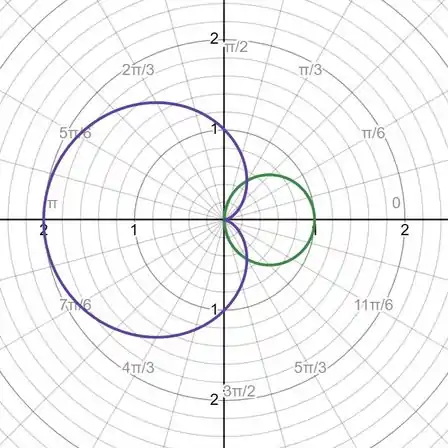
Gráfico das funções: