Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 35
Encontre a área dentro do laço maior e fora do laço menor da limaçon
Passo 1
A área de uma curva em coordenadas polares é dada por
Antes de mais nada, vamos desenhar essa curva aí pra gente visualizar a área que teremos que calcular.
Com a ajuda no nosso bom e velho Winplot:
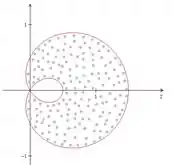
Queremos essa área pontilhada aí.
Mas, se você reparar, nossa figura é simétrica, então dá pr dividir essa área em dois e calcular só metade dela e depois multiplicar por dois, certo?
Passo 2
Ok, agora vamos pensar o intervalo de integração.
Quando , temos
Estamos nesse ponto azul
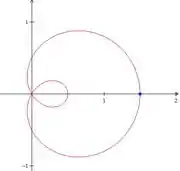
Quando , temos
Estamos no ponto verde:
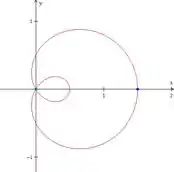
Assim, podemos integrar nossa curva de até .
Só que com isso, a gente pega também esse loopingzinho de dentro, que é o tal do laço de dentro, que a gente NÃO quer na nossa área.
Então nesse caso, a gente vai precisar TIRAR a área desse laço interno aí.
Passo 3
Pra tirar a área do laço interno, vamos pensar:
Qual o valor de pra quando vale zero e quandoo está na pontinha do laço menor, ou seja, quando vale (porque o já atingiu zero, então agora conforme aumenta, vai diminuindo, ok?)?
Para , temos que
Show!
E para temos que
Passo 4
Dessa forma, vamos calcular a área da metade de cima do laço maior de até e subtrair a área do laço de dentro de até .
Vamos fazer isso daqui oh:
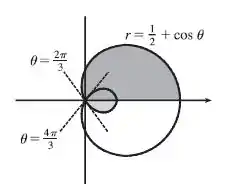
Mas isso vai ser só METADE da nossa área de interesse, que é essa aqui:
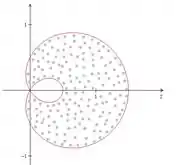
Então no final a gente vai multiplicar isso por 2.
Show de bola?
Passo 5
Vamos a integral.
Assim, a área total é