Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 42
Encontre todos os pontos de interseção das curvas dadas
Passo 1
Fala ai! Vamos iniciar esta questão montando um passo a passo. Assim não vamos nos perder e teremos um caminho a seguir.
Gostaram da ideia? Bora lá!
1 – Construir a curva para termos noção de onde estão localizados os pontos de interseção.
2- Igualar as equações para encontrar os valores de e .
Passo 2
Através de um programa computacial como Geogebra, vamos olhar as duas curvas pras ver o que estamos buscando:
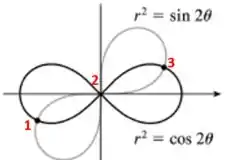
Pela figura, podemos perceber que existem três pontos de interseção entre as duas curvas. Vamos buscar esses pontos.
Igualando as curvas:
Passo 3
Não acabamos por aqui. Como essa tangente veio de equações que envolviam , tanto o seno quanto o cosseno do nosso ângulo tem que ser positivos.
Isso significa que para achar esse que tá no terceiro quadrante, vamos ter que considerar um intervalo de .
Assim, teremos também para tangente igual a 1:
Que tá valendo também.
Okok?
Além disso, pela figura, podemos ver também que a origem também é um ponto de interseção.
Passo 4
Vamos encontrar o valor de . Formando o ponto .
Para isso, é só substituir os valores de em uma das curvas, já que como é um ponto de inteseção, tanto faz a curva que vamos escolher, as duas vão dar o mesmo ponto!
Para :
Para :
Passo 5
Os pontos de interseção são portanto:
Resposta
, e