Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 37
Encontre todos os pontos de interseção das curvas dadas.
37-
Passo 1
Olá, meu nobre e querido amigo. Pronto para resolver essa atividade comigo?
A gente aqui vai encontrar todos os pontos de interseção das curvas:
E para isso, a gente precisa igualar as equações delas, precisamos encontrar os valores de em que elas se encontram, e após isso, iremos substituir esses valores de em qualquer uma das equações, e assim a gente tem os valores de onde esses encontros ocorrem.
Uma outra coisa que devemos fazer é procurar se elas se encontram na origem. Para isso, deveremos igualar as equações a zero, caso ambas possuam valores de para essa condição, quer dizer que elas se encontram na origem.
Passo 2
Primeiramente vamos igualar os das duas equações:
Dividindo por cosseno as duas equações nós teremos:
E teremos essa equação como verdadeira em apenas dois pontos:
E esse valore terão valores de iguais a:
Vamos fazer uma tabela com os ângulos de mais conhecidos e comparar.
E vamos passar essas coordenadas polares para cartesianas:
Para
E para
Logo para nunca poderá assumir valores negativos.
O mesmo raciocínio é válido para a coordenada cartesiana
Onde para teremos logo nunca será negativo para essa função.
O que nos diz então que não poderemos ter como interseção.
Com isso temos nosso ponto polar igual a:
Passo 3
Outra posição de encontro das duas funções é que elas começam na origem com , porém ambas terão angulações iniciais diferentes:
Em coordenadas cartesianas esse ponto será igual a:
Gráfico das duas funções gerado pelo Desmos, para que a gente veja que nossos cálculos estão corretos está abaixo:
Aqui na aba esquerda é onde você coloca a equação da curva que você quer plotar.
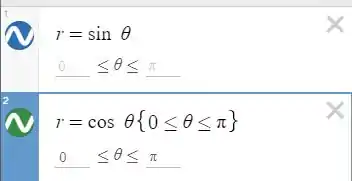
Os valores de em cosseno serão negativos quando passam de tendo valores abaixo de .
Pois os valores de que são iguais a vão ser iguais a nunca sendo negativos.
Os valores de para a função seno serão negativos quando passam de e somente terá termos positivos em , pois ficará igual a nunca sendo negativos em