Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 57
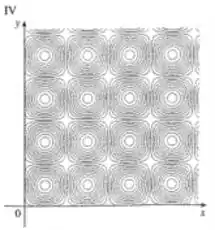
Case a função com seu gráfico (indicado por na página 899) e com seus mapas de contorno (indicado por ). Dê razões para sua escolha.
57-
Passo 1
E aí, pessoal. Tudo certo?
Nessa questão, precisamos analisar a função dada e comparar com os gráficos mostrados na página 899, os quais podem ser vistos aqui:
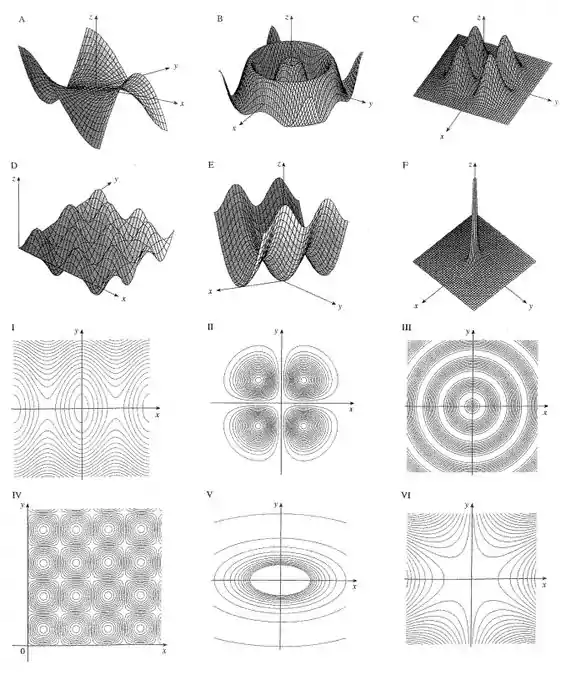
Após dizer qual é o gráfico, de A até F, vamos dizer também qual é o mapa de contorno para o gráfico escolhido.
Tranquilo? Vem comigo.
Passo 2
A função
é uma função de duas variáveis, dada pelo produto de duas funções seno. Nós sabemos que essas funções são limitadas entre e . Então, a função
também estará limitada entre e . Além disso, a função tem periodicidade tanto em quanto em .
Passo 3
Como podemos visualizar o gráfico de ?
Imagine que fixamos e vamos deixar variável. Nós teremos uma função
que agora é uma função apenas de . Dessa forma, para todos os valores possíveis de , no plano teremos o gráfico de uma função seno.
Da mesma forma, podemos fixar . Teremos a função
que vai dar origem a função seno no plano quando . Podemos fazer isso para todos os valores de do domínio da função .
Passo 4
Com essa descrição, o único gráfico que faz sentido é a de letra (mesmo que esteja só no primeiro quadrante, a função pode englobar todos os quadrantes sem problemas).
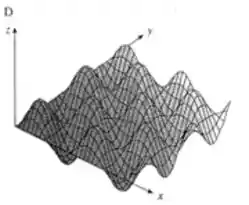
E a única de nível condizente é de número .
