Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 29

x 2 + 2 y 2 = k 2

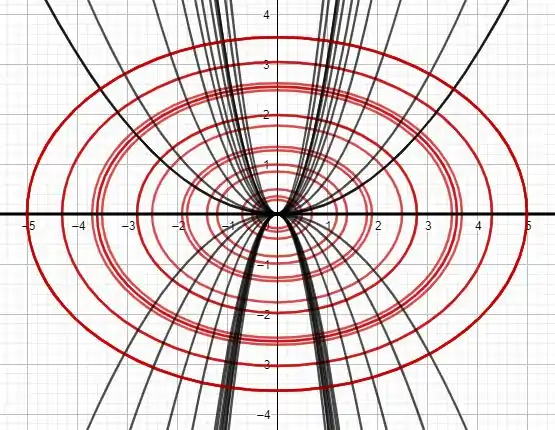
Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.

Passo 1

Bom, galera. Aqui o exercício fala em trajetórias ortogonais. Parece um nome complicado, mas calma que a gente já vai entender juntos.

“Ortogonal”, relembrando, dá a ideia de que duas coisas fazem 90 ° entre si. Quais seriam essas coisas aqui no nosso exercício? Bom, uma é a curva que o enunciado nos deu: x 2 + 2 y 2 = k 2 , e a outra é justamente o que ele nos pede, a tal da trajetória ortogonal.

Mas o que significaria duas curvas fazerem 90 ° entre si? A gente vai olhar se em cada ponto em que elas se cruzam, suas inclinações fazem 90 ° entre si. Então, nosso foco vai ser trabalhar com as derivadas dessas curvas, beleza?

Passo 2

Bora ver como é a inclinação (ou derivada) da curva do enunciado? Pra isso, vamos pegar a equação e derivar os dois lados em relação a x . Lembre que y depende de x , então temos que usar a regra da cadeia, mas k é uma constante e sua derivada se anula.

x 2 + 2 y 2 = k 2

2 x + 2 .   2 y d y d x = 0

d y d x = - 2 x 4 y = - x 2 y

Passo 3

Agora que sabemos a inclinação da curva do enunciado, como encontrar a inclinação da trajetória ortogonal? A gente pode usar o fato de que duas retas formam 90 ° se a inclinação de uma é, ao mesmo tempo, oposto e inverso da inclinação da outra. Ou seja, pra achar a derivada da trajetória ortogonal, é só trocar o sinal e inverter a fração da derivada da curva do enunciado:

d y d x = 2 y x

Passo 4

No passo anterior, encontramos a derivada da trajetória ortogonal, e isso nos deu uma informação muito da hora: uma equação diferencial separável que representa a curva que queremos encontrar. Bora resolver?

d y d x = 2 y x

1 y d y = 2 x d x

∫ 1 y d y = ∫ 2 x d x + C

l n y = 2   l n x + C

Agora a gente usa algumas propriedades de logaritmo e módulo pra dar aquela ajeitada na nossa equação:

ln ⁡ y = l n | x | 2 + ln ⁡ C

ln ⁡ y = l n   x 2 + ln ⁡ C

ln ⁡ y = ln ⁡ C x 2

y = C x 2

y = C x 2

Chegamos numa expressão até bonitinha pra nossa trajetória ortogonal, não é mesmo? É uma família de parábolas. Pra você ver como faz sentido chamá-la de “ortogonal”, olha esse desenho com as duas famílias de curvas, olha como elas realmente parecem fazer 90 ° em cada ponto!

Resposta

y = C x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

y = x 1 + k x Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
y 2 = k x 3 Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
y = k x Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.8 - 2 x 2 + y 2 = c 2
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.6 - y = c x 2