Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 29
Encontre três diferentes superfícies que contém a curva: .
Passo 1
Nesse exercício, temos a curva parametrizada:
E precisamos encontrar diferentes superfícies que contenham essa curva.
Se colocarmos a nossa curva em coordenadas cartesianas relacionando duas componentes da mesma curva, teremos uma curva que em duas dimensões que contêm a nossa curva . Sei que parece confuso, mas irei te ajudar a visualizar.
Nesse exercício, temos:
Dessa forma, isolando da equação em , temos:
Passo 2
Com isso, podemos agora substituir essa relação na equação para :
Dessa forma, a curva está sob o cilindro . Podemos agora realizar o mesmo procedimento substituindo o valor de na equação para , obtendo:
Então a curva também fica sob o cilindro .
Passo 3
E, por fim, da equação em , podemos reescrever:
Da equação em , temos que , dessa forma, substituindo essa expressão na equação anterior, obtemos:
Dessa forma, a curva também fica sob o cilindro parabólico .
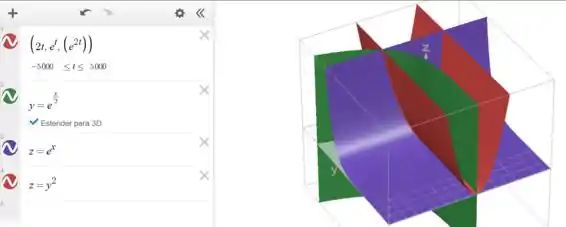
Podemos visualizar no desmos que estamos certos nas nossas considerações:
