Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.1 - Ex. 4
O ponto pertence à curva
- Se é o ponto , use sua calculadora para determinar a inclinação da reta secante , com precisão de 6 casas decimais, para os seguintes valores de
- 2,5
- 2,9
- 2,99
- 2,999
- 3,5
- 3,1
- 3,01
- 3,001
- Usando os resultados da parte (a), estime o valor da inclinação da reta tangente à curva no ponto .
- Utilize a inclinação obtida na parte (b) para achar uma equação da reta tangente à curva em .
- Esboce a curva, duas das retas secantes e a reta tangente.
Passo 1
Fala gente bonita!
Nessa questão temos uma curva que é dada por e sabemos que o ponto pertence a essa curva.
Depois, temos o ponto que é dado por . Ou seja, esse ponto também pertence a curva e ele varia para cada valor de dado.
Para a letra , vamos encontrar os pontos para os valores de dado e então encontrar a inclinação da reta secante , para isso vamos usar a fórmula da inclinação de uma reta entre dois pontos.
Sendo e as coordenadas do ponto e e as coordenadas do ponto .
Depois vamos transformar essa reta secante numa reta tangente, isso é, aproximar ao máximo o ponto do ponto , fazer isso vai ficar mais fácil com os resultados da letra a.
Assim estimaremos um valor para a inclinação da reta tangente e com isso poderemos encontrar uma função reta tangente no ponto que é dada por:
Onde e .
Bora lá então!
Passo 2
Letra a)
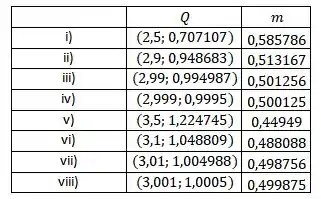
Primeiramente, calcularemos os valores de para cada dado, daí ficamos com
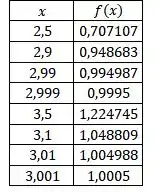
Agora, utilizando a fórmula
Temos que é o ponto , daí
E temos que e são as coordenadas do ponto que estão na tabela.
Calculando por exemplo o para o valor , obtemos:
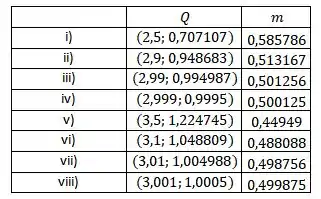
Agora calculando todos os e colocando em uma tabela, ficamos com
Passo 3
Letra b)
Para calcular o da reta tangente, precisamos aproximar o ponto do ponto . Ou seja, a coordenada de Q deve se aproximar de e a coordenada deve se aproximar de 1.
Pela tabela, podemos ver que quando e , temos que .
Daí, podemos estimar
Passo 4
Letra c)
Temos que a equação da reta tangente em um ponto é dada por
Substituindo os valores do ponto e a inclinação , temos
Passo 5
Letra d)
Para esboçar os gráficos das retas, eu vou usar a função da reta que passa pelo ponto
E usar os encontrados nos passos anteriores.
Reta secante entre e , onde temos o
Resolvendo temos
Reta secante entre e , onde temos o
Resolvendo temos
E por fim, para a reta tangente no ponto , temos o .
Resolvendo:
Plotando tudo isso, junto com a nossa função , temos:
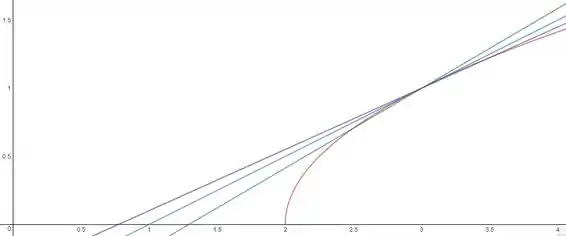
Onde a curva em vermelho representa , a curva em azul é a reta tangente ao ponto , a reta verde é a reta secante ao ponto e a reta roxa é a reta secante ao ponto .
