Encontre o valor exato de cada expressão.

Vamos começar aplicando as propriedades do logaritmo na expressão do item (a):

Observe a propriedade , no passo , e repare que a subtração entre logaritmos significa que os números estavam incialmente divididos. Então, podemos escrever:

A soma entre eles indica que eles estavam inicialmente sendo multiplicados:

Vamos lembrar que só podemos aplicar estas propriedades porque todos os termos estavam na base .

Agora vamos usar a propriedade :

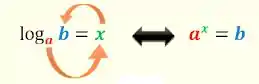
Fazemos esse círculo e pronto. Bora tentar?

Fatorando :

Ou seja,

Para a letra (b) faremos a mesma coisa, usando a expressão:

Escrevendo essa subtração como um quociente:

E fazendo isso novamente:

Então, fazendo a divisão de frações:

Agora usando terceira propriedade e transformando isso em potência, temos:

Fatorando o :

Isso é o mesmo que:

Logo, temos:

Valeu, galera! Até a próxima! 😉