Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 66b
Encontre o valor exato de cada expressão.
Passo 1
Fala, galerinha!
Temos uma questão bem direta ao ponto! Precisamos encontrar o valor exato de:
Relembrando, o , famoso arco cosseno, é a função que diz qual ângulo tem cosseno igual a . Ou seja, pra calcular o , precisamos determinar qual ângulo tem cosseno igual a .
Vem comigo que vamos ver direitinho como fazer isso!
Passo 2
Queremos descobrir qual ângulo tem cosseno igual a . Vamos dar uma olhadinha em como fica no bom e velho Círculo Trigonométrico!
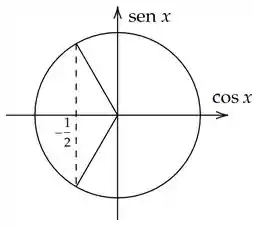
Olha só. Na figura, marcamos no eixo do cosseno (horizontal) o valor e traçamos os ângulos correspondentes.
Pela figura percebemos que de até , os ângulos que estamos procurando são e .
Mas será que podemos considerar os dois?
Passo 3
Pra responder essa pergunta, precisamos lembrar que a função só pode assumir valores de até . Essa é uma definição importante que precisamos guardar na cabeça, tá bem?
Isso significa que dos ângulos que tem cosseno igual a , estamos procurando o , ou em radianos, .
Então podemos dizer que: