Encontre o valor exato da quantidade dada:

Fala povo, tudo certo? Vamos começar de dentro pra fora, tudo bem? Imagina que temos:

Como, lendo isso, temos que é o arco cujo cosseno é , podemos reescrever isso de forma a trabalhar sem inversas. Ou seja:

A gente pode montar um triângulo auxiliar com esse resultado viu? Logo, usando como o valor do arco, temos:

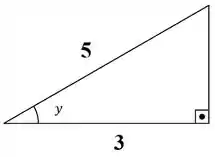
Por Pitágoras, completamos esse triângulo:

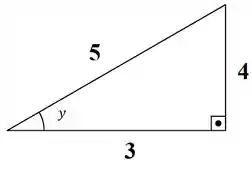
E galera, olha o pulo do gato. Como a questão quer:

E nós chamamos:

Então basta a gente encontrar ! Mas como:

Do triângulo auxiliar, temos:

E por fim, chegamos a resposta!!