Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 7
- A figura abaixo mostra o gráfico de uma função sobre seu domínio . Explique por que tem uma inversa e use o gráfico para encontrar , e .
- Encontre o domínio e a imagem de .
- Esboce o gráfico de .
Passo 1
Letra a)
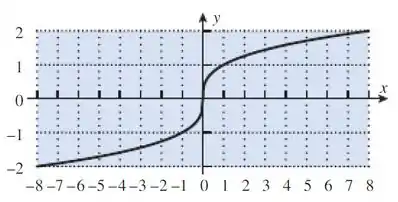
Fala galera, tudo na paz? Vamos trazer aqui rapidinho o gráfico da questão:
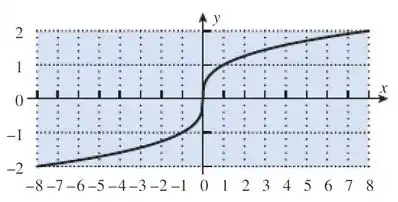
A letra a quer da gente uma explicação do porque essa função com certeza tem inversa. Bem, pra uma função ter inversa, ela tem que ser injetora e sobrejetora ao mesmo tempo. Pra isso, deve valer:
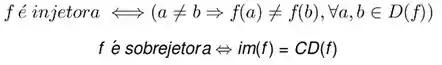
Eita que enrolado! Hahahaha calma galera, basicamente isso quer dizer que não vai existir nenhuma valor de nessa função que pode ser encontrado usando valores diferentes de e que a função tem imagem e domínio coincidente. Pô, olhando pro gráfico do enunciado dá pra ver que é o nosso caso! Então ta de boas! Um truque vai ser que: toda função estritamente crescente ou decrescente em seu domínio é sempre bijetora, logo invertível.
A letra ainda pede mais coisa. Ela quer saber:
Bem, como, olhando pelo gráfico, temos:
Pra gente achar o que a questão pede basta entender esses resultados como pontos
E como tamos falando de inversas, a gente troca de lugar:
O que é o equivalente a:
Passo 2
Letra b)
Bem, a questão pede domínio e imagem da inversa. Bem, vamos olhar de novo pro gráfico da função:
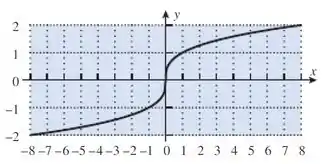
Através dele a gente consegue tirar o domínio e imagem de f, mas calma que não é isso que queremos, vamos trabalhar com ele depois:
Po galera, pra inversa, literalmente é só inverter hahaha. Afinal, da definição de função inversa, temos:
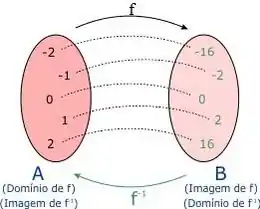
Sendo assim, ta na mão:
Passo 3
Letra c)
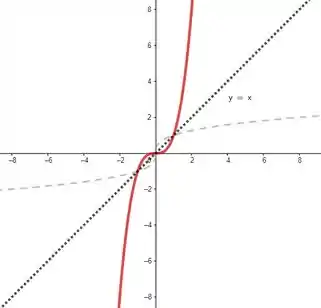
Pra esboçar esse gráfico a gente pode usar uma estratégia bacana: funções inversas são imagens espelhadas de suas funções originais em relação ao eixo ! Portanto um esboço pra inversa da nossa função seria a função em vermelho abaixo:
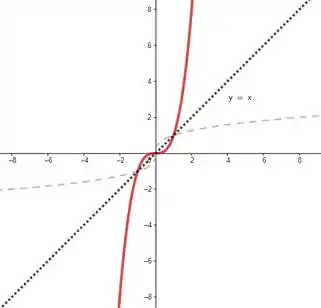
Resposta
a) A função tem inversa por ser bijetora. Podemos ainda concluir isso ao vermos que ela é estritamente crescente, o que implica em ser bijetora e, logo, invertível.
