Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 33
Verdadeiro/Falso
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta
33) Uma função injetora é invertível.
Passo 1
Fala povo, tudo certo? Tão nos perguntando se uma função injetora é invertível. Bem, quando a gente inverte uma função, nós fazemos isso:
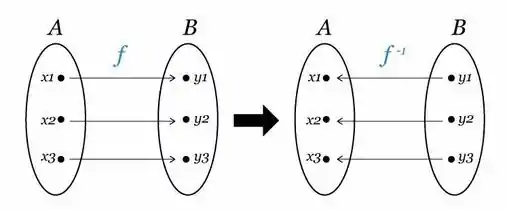
Logo:
- Se era domínio de , então, ao invertermos, vira imagem de
- Se era imagem de , então, ao invertermos, vira domínio de
Bem, uma função injetora é aquela que cada conjunto possui uma única associação possível. Ou seja, não tem como dois diferentes darem o mesmo como está acontecendo abaixo mas não acima:
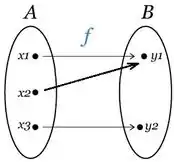
Afinal, como eu iria inverter esse cara acima? Quando eu fosse voltar de pra , pra onde eu iria?
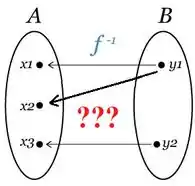
Então ok, já sabemos que a função precisa ser injetora pra ser invertível. Porém será que isso é o suficiente?
Passo 2
Uma função pode ser, além de injetora, sobrejetora, certo? Isso significa que contradomínio e imagem coincidem, caso ela seja também, o que é o caso dessa imagem que usamos no Passo 1:
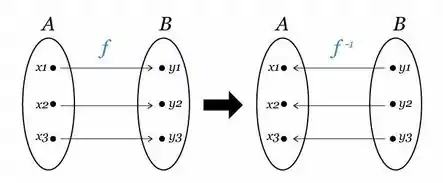
Então aqui, a função é bijetora (injetora e sobrejetora ao mesmo tempo). Mas e se fosse injetora, mas não sobrejetora? Teríamos algo como:
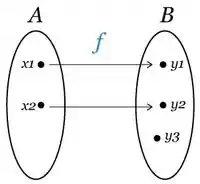
Se olharmos a função como uma máquina que transforma em , onde:
- Domínio de
- Contradomínio de
- Caso 1) Existir um elemento do que não associa a nenhum do É como se a máquina dissesse que você pode inserir algum elemento de , aí você faz isso e ela não te devolve nada. Tipo aquelas moedas que ficam perdidas no fliperama hahaha. Não ta certo isso né?
- Caso 2) Existir um elemento do que não associa a nenhum do É como se a máquina dissesse pra você que ela é incapaz de produzir esse elemento de , mas admitisse sua existência. É esperado que ao colocar uma moeda no fliperama você não receba um sorvete, certo?
- Contradomínio de
- Domínio de
Teríamos:
Bem, se a gente olhar pra imagem acima, vemos que o caso não acontece, mas o caso acontece, o que está de boas! Maaaaas, ao invertermos esse :
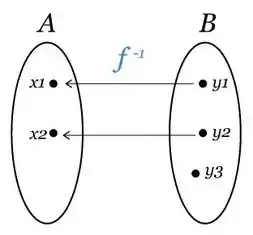
Onde, aqui:
E olha só! O caso passa a acontecer agora, e o caso não! Como a situação não pode acontecer pra função nenhuma, se ele acontece, não temos uma função. Em resumo: uma função precisa ser sobrejetora pra que possa existir. Como o enunciado não fala nada sobre ser sobrejetora também, então é falsa a afirmação.
Resposta
Falsa