Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 28

Esboce a região delimitada entre as curvas e visualmente estime a localização do centroide. Em seguida, calcule as coordenadas do centroide.

y = s e n x     ,       y = 0 ,     0 ≤ x ≤ π

Passo 1

Vamos esboçar o centroide, beleza ?

Olhando para as funções dadas, dá pra ver que teremos uma região entre uma retas e algo parecido com uma parabola. Bora desenhar então.

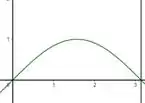
Passo 2

Vamo ligar o chutomêtro agora shihih. Vamos adivinhar onde está o centroide.... Olhando bem para o desenho, podemos chutar     x - = 1,5     e   y - = 0,5

Passo 3

Bora ver se nosso olho ta bom. Ou seja, vamos para as contas.

Sabendo que

x - = 1 A ∫ 0 1 x [ f x - g x ] d x

E,

y - = 1 A ∫ 0 1 [ f x ] 2 - g x 2 d x

Onde A   é área entre as funções.

Vamos achar logo a área , bb! Como temos uma so curva, cuja interseção com x = 1 é em x = 0   e x = 1 ,

A = ∫ 0 π s e n   x     d x = - cos ⁡ x 0 π = 1 - - 1 = 2

Daí,

x - = 1 2 ∫ 0 π x ( s e n   x   ) d x = 1 2   - x c o s x   ​ 0 π - ∫ 0 π - cos ⁡ x   d u   = 1 2   π + s e n   x ​ 0 π     = 1 2 π

E,

y - = 1 2 ∫ 0 π s e n   x 2 d x = 1 2 ∫ 0 π 1 2 [   1 - cos ⁡ 2 x ]   d x   = 1 4   x + 1 2 s e n 2 x 0 π = π 4

Então o centroide é

x - , y - = π 2 , π 4

Resposta

x - , y - = π 2 , π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache x 0t a lq u ef xt e n h av a l o rm é d i o ,c o mxn oi n t e r v a l o[ 3,0 ] é f x = 9 - x ² ²
Ache x0 tal que f(x) tenha valor médio, com x no intervalo [4,0] f x = 8 x - x ² ²
Determine o valor médio de ln ⁡ x em [ 1 , e ] .
É verdade que o valor médio de uma função integrável em um intervalo de comprimento 2 é a metade da integral da função ao longo do intervalo? Justifique sua resposta.
Verifique que ∫ ln ⁡ xd x = x ln ⁡ x - x + C .