Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 40
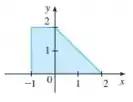
Encontre o centroide da região mostrada, não por integração, mas por localização dos centroides dos retângulos e triângulos (do Exercício 39) e usando a aditividade dos momentos.
Passo 1
Vamos entender esse problema: Bom, o centroide como o próprio nome já nos diz é o centro de massa da região em análise. No nosso caso temos duas figuras a serem estudadas, o triângulo e o retângulo.
Para o retângulo temos que o centroide é localizado no ponto e a área é . Já o triângulo, tem área e centroide .
Para os cálculos usando a aditividade dos momentos, temos
Agora podemos substituir na fórmula e fazermos os devidos cálculos!!
Passo 2
Calculando a coordenada em ,
Agora em y,
O centro de massa possui coordenadas .
Resposta
.
Exercícios de Livros Relacionados
Suponha que uma bola saia do repouso e após t segundos sua velocidade seja V m/s. Desprezando a resistência do ar, expresse V em termos de t como v = f(t) e ache o valor médio de f [0,2]. (sugestão :
Suponha que F seja continua em [a,b] e ∫ b a f ( x ) d x = 0 . Prove que existe pelo menos um numero c em [a,b] tal que f(c) = 0
Mostre que se g(x) = 1, o teorema ∫ b a f ( x ) g ( x ) d x = f ( x 0 ) ∫ b a g ( x ) d x , torna-se o teorema do valor médio para integrais.
Ache o valor médio da função f definida por f(x) = 49 - x ² ², no intervalo [0,7]. Faça uma figura. (Sugestão : ache o valor da integral definida, interpretando-a como a medida da área da região encer
Use ∫ b a f x g xd x = f x 0 ∫ b a g xd x p a r ap r o v a rad e s i g u a l d e ∫ - 1 / 2 1 / 2 s e n 2 π x c o s ( π x )d x ≤ ∫ - 1 / 2 1 / 2 c o s ( π x )d x