Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 43
Se é uma região limitada pelas curvas , determine o valor aproximado da integral . (Utilize uma ferramenta gráfica para estimar os pontos de intersecção das curvas.)
Passo 1
Oi, gente! Tudo em ordem?
A questão quer que a gente calcule:
Onde é a região limitada pelas curvas:
E:
Usando uma ferramenta gráfica para estimar o ponto de interseção das duas curvas.
Para resolver essa questão precisamos dos limites de integração, que obtemos da descrição da região e é justamente nessa determinação dos limites que vamos precisar achar a interseção das curvas, e pra isso vamos usar uma ferramenta matemática como o GeoGebra ou outros softwares gráficos.
Com os limites de integração em mãos, é só resolvermos nossa integral dupla de forma iterada, ou seja, de dentro pra fora!
Vamos lá!
Passo 2
Seguindo a sugestão dada no enunciado vamos utilizar um software matemático pra plotar as duas curvas e, assim, estimarmos a intersecção entre as mesmas. Sendo assim, plotando em um gráfico ambas as curvas temos:
Obtendo a interseção das curvas no Geogebra:
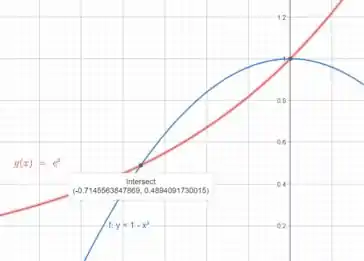
Temos que as curvas de intersectam em
e em
Como
em , podemos escrever nosso limite de integração como uma região do tipo , onde está entre duas constantes e entre duas funções:
Passo 3
Agora é só resolvermos nossa integral:
Integrando em que é a integral de dentro, e aplicando os limites de integração:
Agora integrando em :
Aplicando os limites, teremos:
E prontinho, tá resolvido nosso problema.