Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.2 - Ex. 38
a) Se , encontre .
b) Verifique que se sua resposta da parte (a) é razoável comparando os gráficos e .
Passo 1
E aí! como vai?
Nesse problema foi dada a função
E nosso objetivo é calcular e esboçar os gráficos de e para compara-los.
Parece complicado?
A primeira coisa que podemos perceber quando vemos a função é que se trata de uma razão entre duas funções de .
Por isso, para simplificar nossa vida podemos usar a regra do quociente.
Então bora encontrar e e substituir em .
Bora lá!
Passo 2
Comparando com a função da regra do quociente, podemos perceber que e .
Em ambas as derivadas vamos calcular pela regra da potência.
Substituindo em , temos
Simplificando...
Tranquilo até aqui?
Passo 3
Agora temos que esboçar os gráficos de e .
Começando por , temos
Perceba que temos duas assíntotas verticais nessa função... uma em e outra em . Em ambos os casos, podemos perceber que quando se aproxima pela direita, a função é positiva ( tende a ) e quando nos aproximamos pela esquerda a função é negativa ( tende a ).
Quando , e quando tende a podemos aproximar a função para e portanto é uma assíntota.
Sacou?
Agora vamos analisar a função
Perceba que podemos reutilizar praticamente as mesmas características... a diferença é que agora todo o denominador está ao quadrado e portanto em ambas as assíntotas verticais a função vai tender a nos dois lados pois o numerador será negativo.
Portanto, esboçando os gráficos, em vermelho temos os gráfico de e em azul o de :
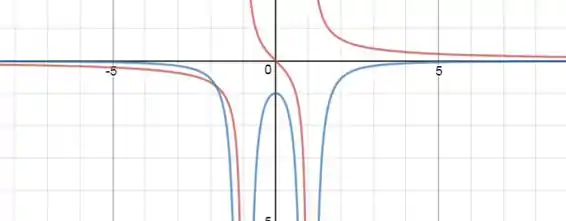
Observe que a curva azul é sempre negativa (abaixo do eixo ) e a curva vermelha é sempre descrescente. Além disso, as duas curvas explodem nos mesmos pontos. Assim nossa resposta para a deriva de é bem razoável, pelo menos graficamente.
E aí! entendeu tudo? Responde Aí!