Seguindo as etapas apresentadas em fazer um esboço do gráfico da seguinte função:
Passo 1
O primeiro passo é determinar o domínio da função, ou seja, .
A nossa função possui duas indeterminações, ou seja, ela não existe em , pois esses valores zeram o denominador e divisão por não é definido. Logo:
Passo 2
Podemos agora determinar os pontos de intersecção com os eixos.
A intersecção em é mais simples de se determinar pois ocorre em .
A intersecção em , é dada para :
Passo 3
Agora vamos determinar os pontos críticos da função. Para isso basta calcular a primeira derivada da função, iguala-la a zero e isolar a variável .
Temos então que:
As raízes de são complexas, logo não temos pontos críticos.
Passo 4
O próximo passo é determinar os intervalos de crescimento e decrescimento de .
Como , a função é sempre decrescente.
Passo 5
Vamos determinar os pontos de máximos e mínimos relativos. Podemos aplicar o teste da segunda derivada.
O teste da segunda derivada diz que:
- Se , tem um valor máximo relativo em .
- Se , tem um valor mínimo relativo em.
Porém como não temos pontos críticos, não temos pontos de máximos nem mínimos.
Passo 6
Determinando agora a concavidade e os pontos de inflexão, ainda pelo teste da segunda derivada.
Por definição a concavidade de uma função pode ser analisada de acordo com a sua segunda derivada. Se é uma função contínua em um certo intervalo e derivável até 2ª ordem no intervalo , temos que:
- Se
- Se
Fazendo temos:
Fazendo temos:
Passo 7
Devemos analisar se a função possui assíntotas. Como nossa função possui dois pontos de indeterminação, precisamos calcular o limite da função com , e .Se o resultado do limite for infinito quando ela tender a infinito, ela não possui assíntota. No caso do limite tendendo a um número de indeterminação da função, se o limite resultar em infinito, a função tem uma assíntota naquele ponto. Assim:
Logo a função possui assíntotas verticais em e e uma assíntota horizontal em .
Passo 8
Por fim, esboçamos o gráfico da função:
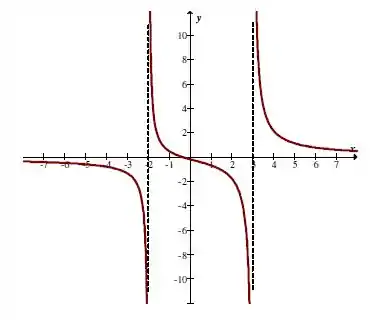
Resposta
Ei, a resposta está no passo a passo :)