Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.2 - Ex. 37
a) Se , encontre .
b) Verifique que se sua resposta da parte (a) é razoável comparando os gráficos e .
Passo 1
E aí! como vai?
Nesse problema foi dada a função
E nosso objetivo é calcular e esboçar os gráficos de e para compara-los.
Parece complicado?
A primeira coisa que podemos perceber quando vemos a função é que se trata de uma razão entre duas funções de .
Por isso, para simplificar nossa vida podemos usar a regra do quociente.
Então bora encontrar e e substituir em .
Bora lá!
Passo 2
Comparando com a função da regra do quociente, podemos perceber que e .
A derivada de é obtida pelo teorema fundamental do calculo onde a derivada de é ele mesmo.
Já a derivada de é obtida pela regra da potencia.
Substituindo em , vamos obter
Simplificando...
Podemos simplificar o numerador com o grau do denominador fazendo...
Tranquilo até aqui?
Passo 3
Agora temos que esboçar o gráfico de e para compara-los...
Começando por
Como temos no denominador e com grau impar, quando tende a vamos ter uma divergência onde se o denominador tende a porem negativo e como o numerador em é , a função tende a em e da mesma forma, tende a em .
Quando decresce, para valores negativos, tende a e quando cresce positivamente a função tende a pois tende a mais rapidamente que .
Sacou?
Agora vamos analisar a função
A mesma coisa que vimos anteriormente para serve para tambem, porém, agora o denominador é de grau par, assim quando , o denominador é positivo para ambos os lados e o numerador é negativo, então tende a quando .
Esboçando ambas as curvas, temos que (em vermelho e em azul )
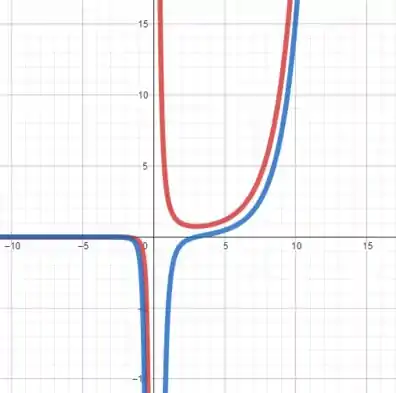
Note que no ponto em que a curva azul se anula, a curva vermelha tem tangente horizontal. Além disso, na região em que a curva vermelha é descrescente, a curva azul é negativa.
Isso corrobora para que nossa resposta do item (a) esteja correta.
E aí! o que achou? Responde Aí!