Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 11
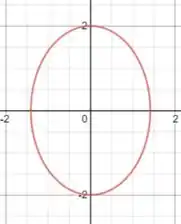
Encontre os vértices e os focos da elipse e esboce seu gráfico:
Passo 1
Falaee, belezinha?? Bom... O enunciado nos deu a seguinte equação que descreve uma elipse:
Queremos calcular os vértices e os focos dessa elipse. Mas o que são eles?
Para responder isso, vamos analisar a figura abaixo de uma elipse:
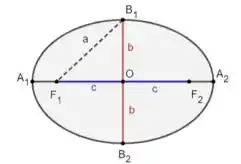
- é o centro da elipse;
- e são seus focos;
- e são as extremidades do eixo horizontal (vértices);
- e são as extremidades do eixo vertical (vértices);
- é a distância entre e ;
- é a distância entre e ;
- é a distância entre e .
Também sabemos que a elipse tem a seguinte equação:
Onde e são constantes e mostradas na figura anterior.
Aplicando essa equação e analisando a nossa definição da elipse, a gente encontra os vértices e os focos. Agora bora lá!! 😉
Ah... lembre-se que os vértices estão sempre em cima de um dos eixos de coordenadas, viu?
Passo 2
Calculamos então o valor de e da nossa equação comparando com a fórmula mostrada no passo 1.
Assim, podemos inferir que:
E
Com isso, percebemos que os vértices da horizontal são:
e
E os vértices da vertical:
e
Logo, percebemos que trata-se de uma elipse com eixo maior na vertical.
Passo 3
Podemos então calcular o valor do foco:
Assim, como a elipse tem lado maior na vertical, os focos são:
Passo 4
Com esses dados, podemos plotar a nossa elipse:
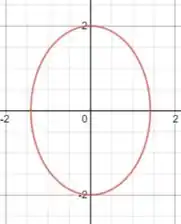
Perceba que os vértices estão exatamente como calculamos 😉
Resposta
Vértices:
e
e
Focos:
e
