Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 7

Encontre a área da região sombreada:

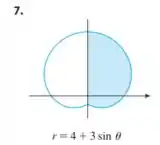
Passo 1

Olá, meu nobre amigo. Vamos analisar essa questão.

Temos aqui a função:

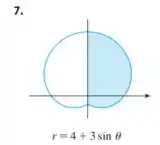
E queremos calcular a área da região sombreada. A equação para encontrar a área de uma curva parametrizada é dada por:

A = ∫ b a 1 2 r 2 d θ

Precisamos determinar o intervalo em que a região se encontra para podermos aplicar os limites de integração na função da área, o intervalo nesse caso será

- π 2 ≤ θ ≤ π 2

Pois estamos caminhando apenas no 1 º e 4 º quadrante.

Então a nossa equação de cálculo de área é:

A = ∫ - π / 2 π / 2 1 2 ( 4 + 3 s e n θ ) 2 d θ

Passo 2

Vamos primeiro resolver a integral indefinida e depois aplicamos os limites:

∫ 1 2 4 + 3 s e n θ 2 d θ

Expandindo o polinômio:

∫ 1 2 16 + 24 s e n θ + 9 s e n 2 θ d θ

Pela linearidade das integrais:

∫ 1 2 16 d θ + ∫ 1 2 24 s e n θ d θ + ∫ 1 2 9 s e n 2 θ d θ

Usando a propriedade trigonométrica:

s e n 2 θ = 1 - c o s 2 θ 2

Ficamos com:

∫ 1 2 16 d θ + ∫ 1 2 24 s e n θ d θ + ∫ 9 4 1 - c o s 2 θ d θ

Integrando termo a termo:

8 θ - 12 c o s θ + 9 θ 4 - 9 8 s e n 2 θ + c

Tirando MMC e somando:

82 θ - 96 c o s θ + 9 s e n 2 θ 8 + c

Passo 3

Substituindo os limites de integração na nossa integral indefinidad:

A = 82 θ - 96 c o s θ + 9 s e n 2 θ 8 - π 2 π 2

A = 82 π 2 - 96 c o s π 2 + 9 s e n 2 π 2 8 - 82 - π 2 - 96 c o s - π 2 + 9 s e n - 2 π 2 8

A = 41 π 4

Resposta

A = 41 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região dentro de um laço, onde r = 1 + 2 s e n θ .
Encontre a área da regiao que e limitada pelas curvas dadas e esta no setor especificado: r = s e n θ,0 ≤ θ ≤ π
Encontre a área da região dentro de um laço, onde r = 3 c o s 5 θ .
Encontre a área da região dentro de um laco, onde r = s e n 2 θ .
Encontre a área da regiao sombreada, onde r = s e n (2 theta) .