Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 14.1 - Ex. 52
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa de contorno da mesma função e compare.
Passo 1
Eae, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos traçar o gráfico dessa função em vários pontos de vista e colocar o que possui melhor visão.
Para isso, basta aplicar o nosso gráfico em uma ferramenta matemática e aí vamos procurar a vista que nos dá mais informações na nossa figura.
Em seguida, devemos plotar as curvas de nível da nossa figura comparando com o gráfico da nossa função.
Agora bora lá!! 😉
Passo 2
Utilizando um software para traçar os gráficos, temos:
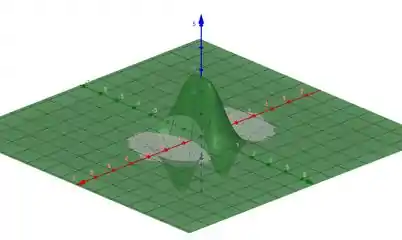
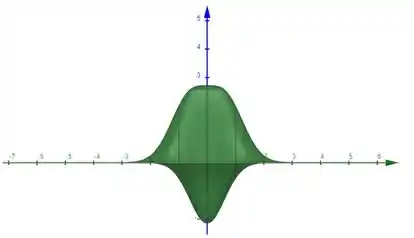
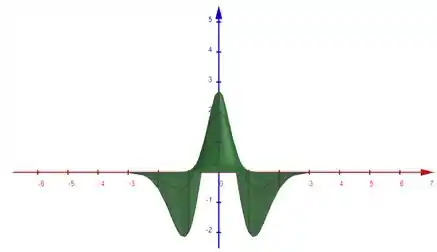
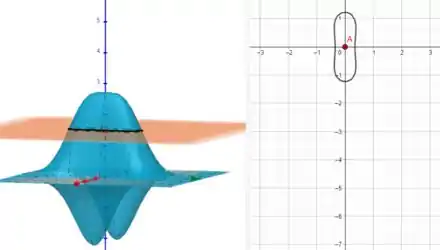
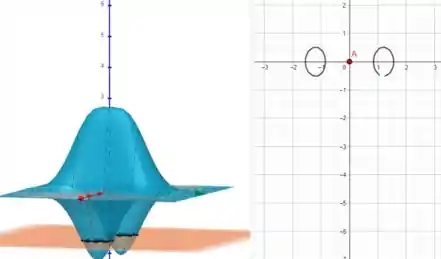
Os últimos dois gráficos nos dão uma visão importante para entender o funcionamento da função em relação a uma das variáveis “isolada”, apesar de que não está totalmente isolada.
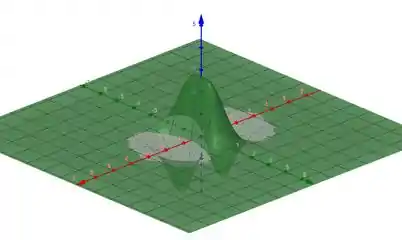
O primeiro gráfico dá uma ideia geral do comportamento da função. Poderíamos pegar outros ângulos, mas, em geral, esse ângulo dá uma boa visão de como a função se comporta.
Passo 3
Agora vamos traçar as curvas de nível da nossa figura escolhida selecionando alguns valores de e comparando ao mesmo tempo com o gráfico da nossa função.
Para , temos:
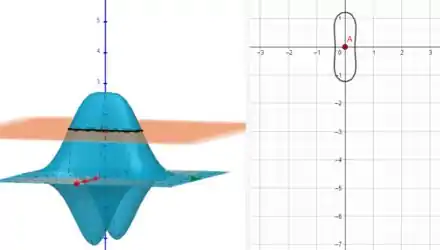
Para , temos:
Para , temos:
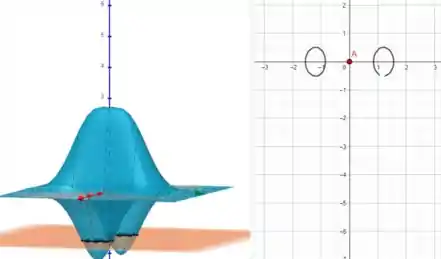
Resposta
