Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 9
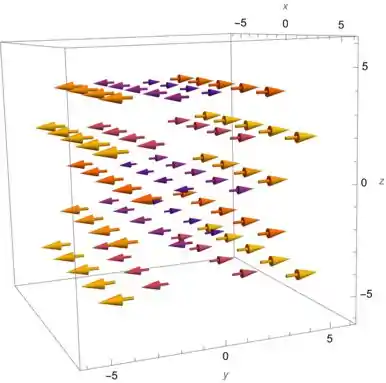
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura
Passo 1
E aii, galera!
Essa questão pede pra gente esboçar um campo vetorial
Com um desenho como dessas figuras:
Como estamos no , nossa figura vai ficar como a .
Pra isso, vamos descobrir como que esse campo se comporta conforme mudamos o ponto .
Então, vamos desenhar alguns vetores pra representar o plano!
Passo 2
Como esse representa a segunda coordenada de , podemos representar o campo assim:
Ou seja, dado um ponto , independente de quem são e , o vetor vai ser .
Isso quer dizer que:
- Para , o vetor aponta na direção positiva de ,
- Para , aponta na direção negativa de , e
- Para , o vetor é , então o campo é nulo.
Além disso, quanto maior o valor de , maior vai ser o tamanho do vetor.
Com isso, conseguimos esboçar o desenho de :
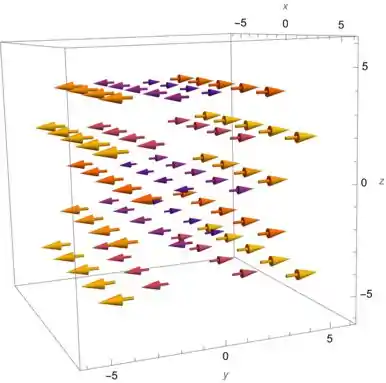
Resposta
Exercícios de Livros Relacionados
Verificar se o campo dado é irrotacional.c) vec f (x , y , z) = (y z e^(x y z) , x z e^(x y z) , x y e^(x y z))
Verificar se o campo dado é irrotacional.e) vec f (x , y , z) = (x^2 , y^2 , z^2)
Verificar se as seguintes funções são harmônicas em algum domínio.b) f x , y = 2 x 2 - y 2 + y + 10
Verificar se as seguintes funções são harmônicas em algum domínio.a) f x , y , z = z x + ln x y
Verificar se o campo dado é irrotacional.d) vec f (x , y , z) = (2 x + cos y z , - x z sen y z , - x y sen y z)