Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 25
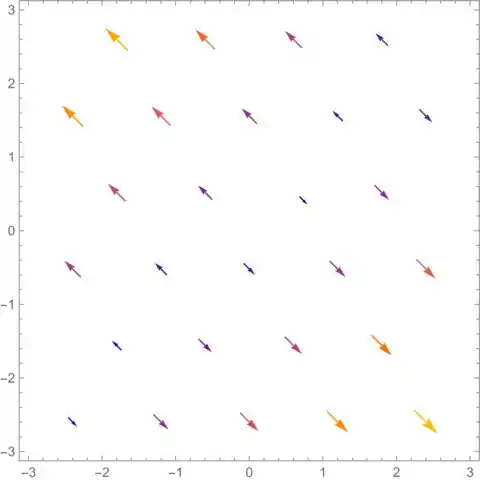
Encontre o campo vetorial gradiente de e o esboce.
Passo 1
Faala galera!
Nesse exercício, precisamos encontrar o campo vetorial gradiente de uma função
E depois esboçar ele.
Precisamos lembrar como calcular o gradiente:
Então a primeira coisa que vamos fazer é calcular as derivadas parciais pra determinar o gradiente.
Depois, precisamos analisar esse campo vetorial, e identificar como ele se comporta conforme variamos o ponto .
Passo 2
Calculando as derivadas parciais:
Primeiro em função de , considerando constante:
Podemos tirar o da derivada, por ser constante, e usar a regra da cadeia:
Então
Agora em função de , com constante:
De novo tiramos e usamos a regra da cadeia:
Então
Assim,
Passo 3
Agora vamos analisar esse campo.
Percebe que quando , as duas componentes valem .
Então, na reta teremos .
Além disso, essa reta divide o em duas regiões:
- Acima da reta, , então e
- Abaixo da reta, , então e
Isso indica que a primeira coordenada do gradiente é negativa, e a segunda positiva. Ou seja, o vetor aponta na direção negativa de (esquerda) e positiva de (cima)
Agora é o oposto: a primeira coordenada do gradiente é positiva e a segunda negativa. Então, o vetor aponta pra direita e pra baixo.
Considerando isso, o campo fica assim:
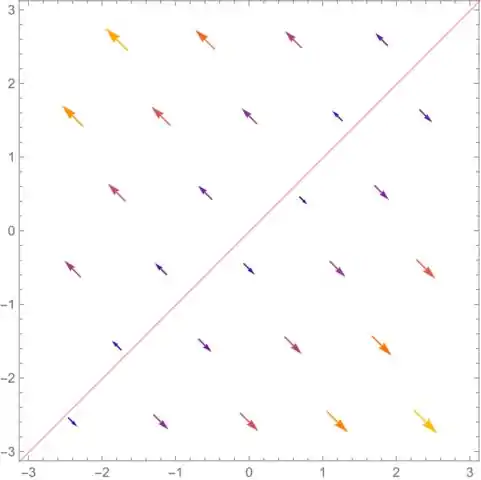
A reta vermelha é .
Resposta
