Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 25
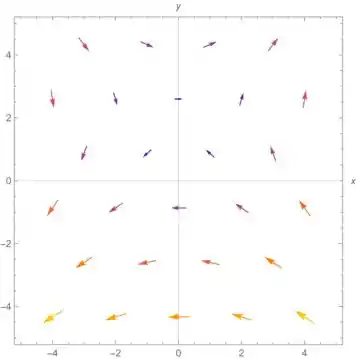
Determine o campo do vetor gradiente de e o desenhe.
Passo 1
Faala, pessoal!
Nessa questão, nós temos uma função de duas variáveis:
E precisamos calcular e desenhar o campo vetorial gradiente.
O gradiente de uma função é calculado assim:
Então, vamos começar calculando as derivadas parciais pra definir o campo gradiente.
Depois, vamos estudar como que esse campo muda conforme mudamos o ponto .
A gente vai precisar olhar pra norma desses vetores:
Assim conseguimos desenhar alguns vetores pra representar o campo.
Passo 2
Bora calcular as derivadas parciais!
Primeiro em função de , considerando como constante:
Agora derivando em função de , com constante:
Então, nosso campo é:
Passo 3
Agora vamos analisar esse campo.
A primeira componente é , então:
- Se , o vetor aponta pra direita (sentido positivo de )
- Se , o vetor aponta pra esquerda (sentido negativo de )
- Se , o vetor é paralelo ao eixo
- Se , o vetor aponta pra cima (sentido positivo de )
- Se , o vetor aponta pra baixo (sentido negativo de )
- Se , o vetor é paralelo ao eixo
Já a segunda componente é , então:
No ponto as duas coordenadas são , é o campo é nulo (não tem vetor)
Resumindo, teremos alguma coisa assim:
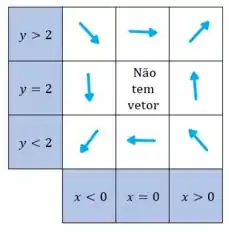
Passo 4
Por último, vamos olhar pro tamanho desses vetores.
A norma de fica assim:
Se elevarmos ao quadrado dos dois lados:
Isso é a fórmula de uma circunferência centrada em .
Ou seja, pontos que têm a mesma distância até terão vetores mesmo tamanho, e quanto mais afastados desse centro, maior serão os vetores.
Com essas informações, desenhamos alguns vetores e temos o diagrama do campo:
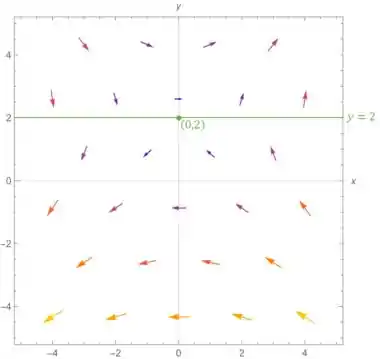
Resposta
