Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 29
Se está no primeiro quadrante e faz um ângulo de com o eixo positivo e , ache as componentes de
Passo 1
Desenhando a situação descrita no exercício, temos o seguinte vetor:
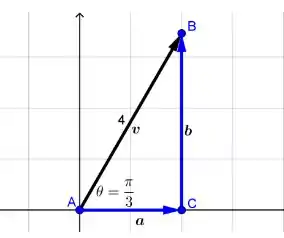
O que nós queremos é encontrar e . Fazendo a decomposição do vetor , sabemos que
Substituindo os valores:
Então a forma do vetor com suas componentes é
Resposta
25.
Exercícios de Livros Relacionados
Sejam w → ≠ 0 → e T o conjunto dos vetores ortogonais a w → . Prove que:(a) w → não pertence a T ;(b) qualquer combinação linear de vetores de T pertence a T;(c) se u → e v → são dois vetores LI de T,
Seja ABCD um retangulo de diagonal BD. Prove que D P → 2 + B P → 2 = A P → 2 + C P → 2 , qualquer que seja o ponto P.
Prove que são verdadeiras as afirmações seguintes.(a) A B → . C D → + B C → . A D → + C A → . B D → = 0 , quaisquer que sejam os pontos A, B, C e D (Relação de Euler).
Sejam a → e b → nao-nulos.(c) Por analogia, tente generalizar os resultados dos itens (a) e (b) para n projeções sucessivas .
As retas que contêm alturas de um triângulo são concorrentes num ponto, chamado ortocentro do triângulo. (Este resultado foi objeto do Exercício 5-21. Sua verificação, com o auxílio da Relação de Eule