Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 60
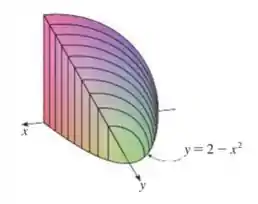
Encontre o volume do sólido descrito por . A base de é a região delimitada por e o eixo . As seções transversais perpendiculares ao eixo são quartos de círculo.
Passo 1
No plano cartesiano temos que a base de é delimitada por e podemos, assim, escrever nossa área em função de como sendo
Assim, nosso volume será calculado como se fosse um círculo completo, porém, dividiremos por 4 pois é um quarto de círculo
Resposta
Exercícios de Livros Relacionados
Conforme a figura abaixo, um copo de coquetel com a forma de um hemisfério com diâmetro de 8c m contém um cereja com 2c m de diâmeto. Se o copo for preenchido até uma profundidade de hc m , que volume
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O método das camadas cilíndricas é um caso especial do método de integração de áreas de seções transversais discutido na Seçã
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O volume de uma camada cilíndrica é igual ao produto da espessura da camada com a área de superfície do cilindro cuja altura
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = x , x = 4 , x = 9 , y = 0