Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 61
Encontre o volume do sólido descrito por . O sólido é delimitado por círculos que são perpendiculares ao eixo , cruzam o eixo e têm centros na parábola .
Passo 1
Eaee, belezinha?? Bom... queremos calcular o volume do seguinte sólido :
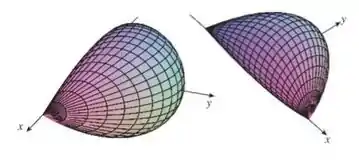
Algumas características desse sólido:
- é delimitado por círculos que são perpendiculares ao eixo ;
- cruzam o eixo ;
- têm centros na parábola .
Podemos determinar o volume da seguinte forma:
Agora vamos aplicar!! 😉
Passo 2
Se temos círculos perpendiculares ao eixo nossa integral é dada em . Assim, teremos
Nosso volume é dado por
Então, substituindo os valores vamos ter
Entendeu direitinho?? Responde aee 😉
Resposta
Exercícios de Livros Relacionados
Se um fluido entra em um tanque semiesférico com raio de 3m , a uma taxa de 0,5m 3 / m i n , com que velocidade estará subindo quando a profundidade for de 1,5m ? [Sugestão Veja o exercicio 55 .]
A figura a seguir mostra as dimensões de uma pequena lâmpada em 10 pontos igualmente espaçados.(a) Use fórmulas de Geometria para fazer uma primeira estimativa do volume englobado pela parte de vidro
A figura abaixo mostra uma calota esférica de raio ρ e altura h cortada de uma esfera de raio r . Mostre que o volume V da calota pode ser expresso como: V = 1 3 π h 2 ( 3 r - h ) V = π h 6 3 e 2 + h
Encontre o volume da cunha descrita no Exercício 61 por fatiamento perpendicular ao eixo x .
Em 1635, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado princípio de Cavalierri: Se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversai