Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 54

Encontre o volume do sólido descrito por . A base de é um disco circular com raio . As seções transversais paralelas perpendiculares à base são quadrados.

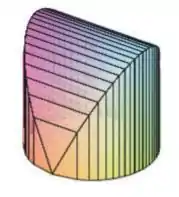
Passo 1

Eaeee, belezinha?? Bom... a questão quer que calculemos o volume do sólido abaixo:

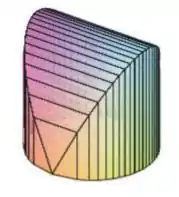
Em que sua base é um disco circular com raio e as seções transversais paralelas perpendiculares à base são quadrados.

Lembrando que ... o volume gerado pela rotação de uma região pode ser calculado através da seguinte expressão:

E aí?? Bora lá?? 😉

Passo 2

Para uma melhor visualização da figura, vamos analisar os cortes transversais:

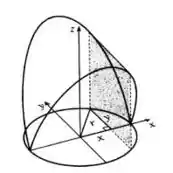
Perceba que os limites de integração são os limites da circunferência, onde:

Ainda, para nosso sólido temos uma base que é um disco circular com raio , mas para nosso caso colocando no plano cartesiano temos a equação da circunferência dada por:

Ou seja, podemos escrever essa área em função de como sendo:

Agora vamos aplicar na integral do volume!!

Passo 3

Assim, nosso volume será dado por:

Entendeu direitinho?? Responde aee!! 😉

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região envolvida por y = x 3 , y = 1 ,x = 0 gira em torno da reta y = 1 .

Nas partes ( a ) a ( c ) , encontre o volume do sólido cuja base é o interior do círculo x 2 + y 2 = 1 e cujas seções transversais tomadas perpendicularmente à base são a Semicírculos b Quadrados ( c

Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d

Descreva o método do fatiamento para encontrar volumes e use-o para deduzir uma fórmula integral para obter volumes pelo método dos discos.

Enuncie uma fórmula integral para encontrar um volume pelo método das camadas cilíndricas e use somas de Riemann para derivar a fórmula dada.