Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 65
Encontre o volume comum de duas esferas, cada qual com raio , se o centro de cada esfera está na superfície da outra esfera.
Passo 1
Opa, bora lá! Nesse problema precisamos calcular o volume comum de duas esferas, cada qual com raio , se o centro de cada esfera está na superfície da outra esfera.
Pra isso precisamos rotacional dois círculos de raio como na figura abaixo:
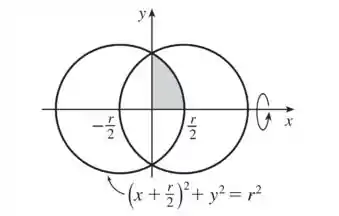
Passo 2
Acharemos o volume da metade direita e posteriormente multiplicaremos por dois, então:
Assim, por simetria, o volume total é
Prontinho!
Resposta
.
Exercícios de Livros Relacionados
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O A C em torno da reta A C
Ache o volume do sólido de revolução gerado quando a região limitada pela curva y = x 3 , pelo eixo x e pelas retas x = 1 e x = 2 é rotacionada em torno do eixo x .
Ache o volume do sólido de revolução gerado quando a região limitada pela curva y = x 2 + 1 , pelo eixo x e pelas retas x = 2 e x = 3 é rotacionada em torno do eixo x .
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O A C em torno do eixo y
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O A C em torno da reta B C