Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.1 - Ex. 7
Derive a função:
Passo 1
Fala aí! tudo certinho?
Bom, galera, precisamos derivar a função. Mas neste caso a função é uma soma de três termos diferente, então acharemos a derivada de cada um separadamente!
Antes de começar as derivadas, a constante pode sair de dentro da derivada. Se lembram?
Agora vamos lembrar de como derivamos pela Regra da Potência:
Veja só! 😉
Passo 2
Tirando as constantes para fora da derivada, temos
Agora pela regra da potência...
Terminando, vamos lembrar de como é a derivada de uma constante:
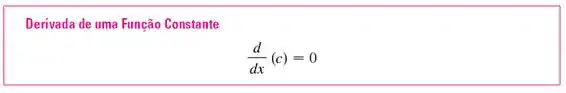
Sendo assim:
E aí! entendeu tudo? Responde Aí! 😎
Resposta
Exercícios de Livros Relacionados
27-28. Use um recurso gráfico para estimar o valor de f ' 1 fazendo um zoom no gráfico de f ; depois compare sua estimativa ao valor exato obtido por derivação.27. f x = x 2 + 1 x
27-28. Use um recurso gráfico para estimar o valor de f ' 1 fazendo um zoom no gráfico de f ; depois compare sua estimativa ao valor exato obtido por derivação.28. f x = x + 2 x 3 2 x
Encontre (d y)/(d x) .y = 4 x^7
Encontre f^' (x) .f (x) = root(3)((8)/(x))
Encontre (d y)/(d x) .y = sqrt(2) x + (1)/(sqrt(2))