Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 16

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica.

y = x 2 , y = 0 , x = - 2 , x = - 1 ao redor do eixo y .

Passo 1

Pra começar vamos entender um pouco melhor as condições que ele nos deu:

y = x 2 , y = 0 , x = - 2 , x = - 1

Esboçando um gráfico, temos:

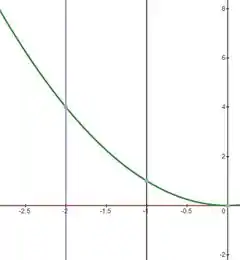
Isso quer dizer que estamos querendo calcular o voluma da região limitada entre os pontos x = - 2 e x = - 1 . Como ele nos pede para rodar em torno do eixo   y , temos:

V = ∫ - 2 - 1 2 π - x f x d x

Esse ( - x ) é porque estamos do lado negativo do eixo x

Logo,

V = - ∫ - 2 - 1 2 π x ⋅ x 2 d x

Isto é,

V = - 2 π ∫ - 2 - 1 x 3 d x

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 2

Integrando, temos:

V = - 2 π x 4 4 - 2 - 1

Assim,

V = - π - 1 4 2 - - π - 2 4 2

Fazendo as contas:

V = - π 2 + 16 π 2 = 15 π 2

Resposta

V = 15 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pelo gráfico de y = 4 x - 1 8 x 4 , pelo eixo x e pela reta x = 2 .
Nos exercícios de 21 a 24, a região é limitada pelas curvas x = y 2 - 2ex = 6 - y 2 gira em torno do eixo indicado. Ache o volume do sólido gerado.23.a reta x = 2
Ache o volume do sólido gerado pela rotação da região limitada pelas curvas y = x 3 e x = y 3 em torno do eixo x. Tome os elementos retangulares de área paralelos ao eixo de revolução.
Ache o volume do sólido gerado pela rotação da região limitada pela curva y = s e n ( x 2 ) , pelo eixo x e pelas retas x = 1 2 π e x = π em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região limitada por aquela reta e pela parábola x 2 = 4 y em torno da reta y = 1 . Tome os elementos retangulares de área paralelos ao eixo de revolução.