Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 57
Encontre o volume do sólido descrito. tem a mesma base do Exercício 58, mas as secções transversais perpendiculares ao eixo são quadradas.
Passo 1
Podemos utilizar o mesmo esboço do exercício anterior:
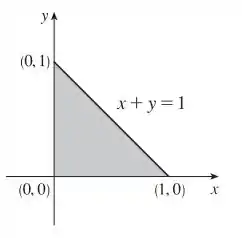
Passo 2
A seção transversal à base correspondente à coordenada tem comprimento . O quadrado com respondente com lado tem área .
Passo 3
Sendo assim, nosso volume é:
Resposta
Exercícios de Livros Relacionados
Um buraco de raio r é perfurado pelo meio de um cilindro de raio Rr com ângulo reto em relação ao eixo do cilindro. Encontre, mas não calcule, uma integral para o volume cortado.
Seja V o volume do sólido obtido pela rotação em torno do eixo y da região limitada por y = x e y = x ² ². Encontre V pelo método de fatiamento e cascas cilíndricas. Em ambos os casos, desenhe um diag
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Explique por que é complicado usar fatias para encontrar o volume V de S . Esboce uma casca de aproximação tí
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume