Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 69

Um buraco de raio r é perfurado pelo meio de um cilindro de raio R > r com ângulo reto em relação ao eixo do cilindro. Encontre, mas não calcule, uma integral para o volume cortado.

Passo 1

Fala aí, galerinha! 😉

Nesse problema temos um cilindro de raio R que possui um buraco de raio r com ângulo reto em relação ao eixo do cilindro.

A partir daí queremos obter a integral do volume cortado do cilindro...

Tem alguma ideia do que fazer? 😐

Tome o eixo x como o eixo do furo cilíndrico do raio r . Um quarto da seção transversal perpendicular y ao eixo y , é o retângulo mostrado abaixo:

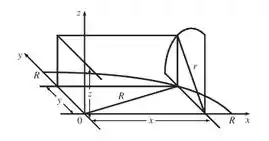
Veja só! 😁

Passo 2

Aplicando o Teorema de Pitágoras duas vezes, nós vemos que as dimensões desse retângulo são:

x = R 2 - y 2

z = r 2 - y 2

Assim, a área é

1 4 A y = x z = R 2 - y 2 r 2 - y 2

e o volume é, portanto

V = ∫ - r r A y d y = ∫ - r r 4 R 2 - y 2 r 2 - y 2 d y

Logo, a integral do volume é dada por

V = 8 ∫ 0 r R 2 - y 2 r 2 - y 2 d y

E aí! O que achou? Responde Aí! 😎

Resposta

V = 8 ∫ 0 r R 2 - y 2 r 2 - y 2 d y

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido descrito por S . A base de S é um disco circular com raio r . Seções transversais paralelas perpendiculares à base são quadrados.
Encontre o volume do sólido descrito por S . O sólido S é delimitado por círculos que são perpendiculares ao eixo x , cruzam o eixo x e têm centros na parábola y = 1 2 ⋅ 1 - x 2 , - 1 ≤ x ≤ 1 .
Uma tigela tem a forma de um hemisfério com 30c m de diâmetro. Uma bola pesada com 10c m de diâmetro é colocada na tigela e a água é derramada na tigela a uma profundidade de h centímetros. Encontre o
Encontre o volume do sólido descrito por S . A base de S é a região delimitada por y = 2 - x 2 e o eixo x . As seções transversais perpendiculares ao eixo y são quartos de círculo.
Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região envolvida por y = 1 / x 3 , x = 1 ,x = 2ey = 0 gira em torno da reta x = - 1 .