Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.3 - Ex. 61

Encontre o volume do sólido gerado quando a região limitada por y = c o s   x , y = s e n   x , x = 0 e x = π 4 gira em torno do eixo x .

Passo 1

Podemos achar o volume de um sólido de rotação em torno de x pela expressão:

V = ∫ a b π f x 2 - g x 2 d x

Onde a nossa região é limitada por g ( x ) (por baixo), por f ( x ) (por cima), x = a e x = b .

Tudo o que a gente precisa fazer é montar essa integral com as informações do enunciado e calcular.

Passo 2

Vamos entender que região é essa olhando num gráfico:

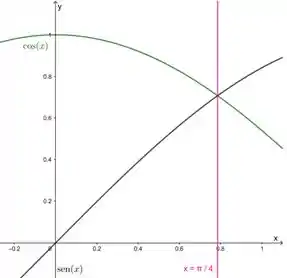
Primeiro vemos que a função que limita ela por cima é y = f x = cos ⁡ x e por baixo a função y = g x = s e n   x . Vemos também que um dos limites de integração é x = a = 0 e o outro é x = b = π 4 .

Agora é só montar a integral:

V = ∫ 0 π 4 π [ cos 2 ⁡ x - s e n 2 x ] d x

Passo 3

Agora é só resolver a integral. Vamos lembrar que:

cos 2 ⁡ x = 1 + cos ⁡ 2 x 2 ,     s e n 2 x = 1 - cos ⁡ 2 x 2

Por isso:

cos 2 ⁡ x - s e n 2 x = cos ⁡ 2 x

Substituindo isso na nossa integral:

V = π ∫ 0 π 4 [ cos ⁡ 2 x ] d x

Usando a substituição u = 2 x :

d u d x = 2 ∴ d u 2 = d x

∫ cos ⁡ 2 x = ∫ cos ⁡ u 2 d u = s e n   u 2 = s e n   2 x 2

Nosso volume fica:

V = π ∫ 0 π 4 [ cos ⁡ 2 x ] d x = π 2   s e n   2 x   ​ 0 π 4 = π 2

Resposta

V = π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral ∫ t g 3 td t
70. Centro de gravidade Determine o centro de gravidade da região delimitada pelo eixo das abscissas, pela curva y = sec ⁡ x e pelas retas x = - π 4 e x = π 4
69. Comprimento de arco Determine o comprimento da curva y = ln ⁡ ( sec ⁡ x ) , 0 ≤ x ≤ π 4
72. Área Determine a área entre o eixo das abscissas e a curva 1 + cos ⁡ 4 x ,0 ≤ x ≤ π
Nos exercícios de 1 a 24, calcule a integral indefinida.12. ∫ cos 6 ⁡ x d x