Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.2 - Ex. 70

70. Centro de gravidade Determine o centro de gravidade da região delimitada pelo eixo das abscissas, pela curva y = sec ⁡ x e pelas retas x = - π 4 e x = π 4

Passo 1

O exercício se refere a essa região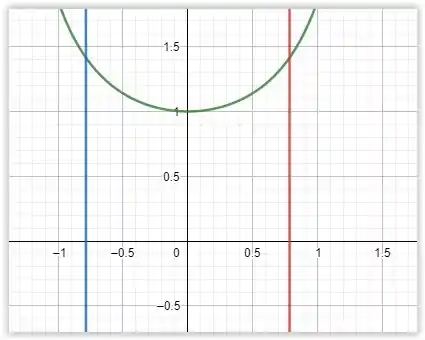

E temos que calcular o centro de gravidade.

Passo 2

Vamos começar calculando a massa da nossa figura, vamos assumir que há uma distribuição homogênea de densidade.

M = ∫ - π 4 π 4 sec ⁡ x   d x   = [ ln ⁡ | sec ⁡ x + t g   x | ] π 4 - π 4

ln ⁡ ( 2 + 1 ) - ln ⁡ | 2 - 1 | = ln ⁡ 2 + 1 2 - 1

Passo 3

Agora vamos calcular o ponto em y onde está o centro de massa

Y c m = ∫ - π 4 π 4 sec ⁡ x   d m ∫ - π 4 π 4 d m = 1 ln ⁡ 2 + 1 2 - 1 ⋅ ∫ - π 4 π 4 sec 2 ⁡ x   2 d x = 1 2 ln ⁡ 2 + 1 2 - 1 ⋅ [ t g   x ] - π 4 π 4

1 2 ln ⁡ 2 + 1 2 - 1 ⋅ ( 1 - - 1 = 1 ln ⁡ 2 + 1 2 - 1

Passo 4

Vamos descobrir o ponto no eixo x.

Não vamos nem precisar calcular nada, apenas reparar na simetria da questão, o ponto em x é 0.

Resposta

O centro de massa está em 0 ,     1 ln ⁡ 2 + 1 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Fórmula ( 27 ) para mostrar que, se o comprimento da curva equatorial em uma projeção de Mercator for L , então a distância vertical D entre as curvas de latitude α ° e β ° do mesmo lado do Equa
( a ) Mostre que ∫ csc ⁡ xd x = - ln ⁡ csc ⁡ x + cot ⁡ x + C ( b ) Mostre que o resultado de ( a ) também pode ser escrito como ∫ csc ⁡ xd x = ln ⁡ csc ⁡ x - cot ⁡ x + C E ∫ csc ⁡ xd x = ln ⁡ tan ⁡ 1
Suponha que o Equador tenha um comprimento de 100c m em uma projeção de Mercator. Em cada parte, use o resultado do Exercício 63 para responder a questão. ( a ) Qual é a distância vertical no mapa ent
Reescreva sin ⁡ x + cos ⁡ x na forma: A sin ⁡ ( x + ϕ ) E use seu resultado junto com o Exercício 65 para calcular ∫ d x sin ⁡ x + cos ⁡ x
Calcule a integral38. ∫ tan ⁡ x sec 5 ⁡ x d x