Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos um caso de rotação de uma região em torno de um eixo. Isso faz com que criemos um sólido, e nessa situação queremos saber o volume do tal sólido.

Vamos representar esse solido graficamente. Para , teremos uma curva com parábola para cima devido ao sinal positivo, como , então

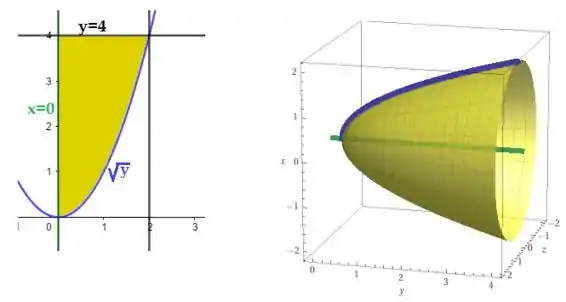
A área da secção transversal desse solido, se vermos ele de frente, como na segunda figura, é uma circunferência

Anote essa área pois iremos utilizar ela para calcularmos o volume do sólido.

Podemos calcular o volume!!