Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

A região é mostrada na primeira imagem. Se girarmos em torno do eixo , obtemos o sólido mostrado na segunda imagem.

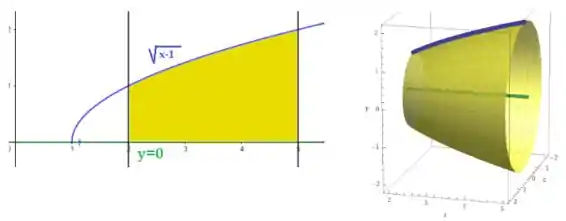
O intervalo de interseção é de , que são as retas mostradas na figura. A área é da secção da rotação .

Onde é o ‘raio’ da circunferência da secção do solido gerado. Veja que na figura dois podemos ver que ao girarmos o solido, e vermos de frente veremos uma circunferência, e é a área dessa circunferência que precisamos.