Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.2 - Ex. 50

Avalie a integral indefinida. Ilustre e verifique se a sua resposta é razoável colocando em um gráfico o integrando e sua antiderivada (C=0).

∫ sin 4 ⁡ x cos 4 ⁡ x d x

Passo 1

Para resolver esse probleminha é bem fácil! Podemos fazer simplificações. Vamos ver:

∫ 1 2 sin ⁡ 2 x 4 d x

1 16 ∫ sin 4 ⁡ 2 x d x

Pronto, mas ainda não tá tudo certo! Aplicamos aquela integral:

sin ⁡ 2 x = - cos ⁡ 2 x 2

Agora ta bom demais!!

Passo 2

Organizando a integral, temos

1 16 ∫ 1 2 1 - cos ⁡ 4 x 2 d x

Então, fica assim:

1 64 ∫ ( 1 - 2 cos ⁡ 4 x + cos 2 ⁡ 4 x ) d x

Resolvemos agora a integral:

= 1 64 x - 1 2 sin ⁡ 4 x + 1 128 ∫ ( 1 + cos ⁡ 8 x ) d x + C

= 1 64 x - 1 2 sin ⁡ 4 x + 1 128 ( x + 1 8 sin ⁡ 8 x ) + C

= 3 128 x - 1 128 sin ⁡ 4 x + 1 1024 sin ⁡ 8 x + C

Analisando o gráfico, temos:

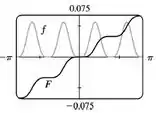
Observe que f x =   0 sempre que F tem uma tangente horizontal. Certinho??

Finishh!! :)

Resposta

∫ sin 4 ⁡ x cos 4 ⁡ x d x = 3 128 x - 1 128 sin ⁡ 4 x + 1 1024 sin ⁡ 8 x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 30, calcule a integral indefinida. 28 )∫ s e n 2 ( π x ) cos 6⁡ ( π x ) . d x
Nos Exercícios de 31 a 36, calcule a integral definida. 36 )∫ π 6 π 4 c o t g ³ w . d w ³
Nos Exercícios de 31 a 36, calcule a integral definida. 31 )∫ π 16 π 12 t g ³4 x . d x ³
Nos Exercícios de 31 a 36, calcule a integral definida. 33 )∫ - π 4 π 4 sec 6 ⁡ ( x ) . d x
Nos Exercícios de 1 a 30, calcule a integral indefinida. 26 )∫ c o s e c 4 ( x ) cotg ²⁡ ( x ) . d x ²