Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 7
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.
Passo 1
Vamos representar esse solido graficamente. Para isso, teremos uma interseção entre as curvas da seguinte forma:
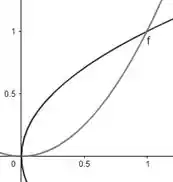
O intervalo de interseção é de (0,1). A área é
Podemos calcular o volume!!
Passo 2
Agora é só calcularmos a integral:
Integrando, temos
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 2 em torno de O A
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 1 em torno de O A
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. x = y 2 ,x = 1 ; em tor
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = 2 - 1 2 x ,y = 0 ,x
Encontre o volume do sólido S descrito.Uma calota de uma esfera de raio r e altura h .