Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 13

Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.

y = x 4 , y = 1 ,   a o   r e d o r   d e   y = 2

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos uma situação onde uma região plana rotaciona em relação a um eixo, isso faz com que agora tenhamos um solido tridimensional.

Vamos representar esse sólido graficamente. Para isso, teremos uma interseção entre as curvas da seguinte forma:

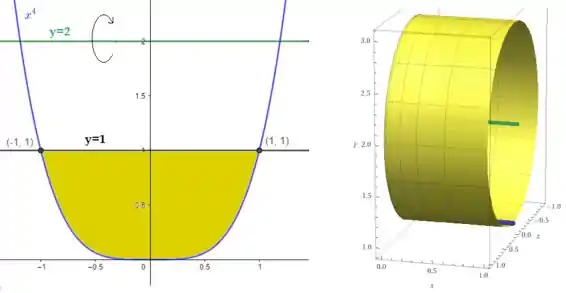
Mas a questão nos diz que essas curvas estão ao redor de y = 2 , sendo portanto, uma medida de raio e caracterizando uma arruela.

Lembramos que a arruela tem um raio interno e outro externo, para termos a seção transversal certa! Ou seja, 2 - 1 e o outro 2 - x 4 .

Então a área pode ser dada por:

A = π 2 - x 4 2 - π 2 - 1 2 = π 3 - 4 x 4 + x 8

Podemos calcular o volume!!

Passo 2

V = ∫ - 1 1 A ( x ) d x

Como os intervalos são iguais, pela simetria podemos calcular apenas uma região e multiplicar o valor por 2:

V = 2 ∫ 0 1 π 3 - 4 x 4 + x 8 d x

Agora é só calcularmos a integral:

V = 2 π 3 x - 4 x 5 5 + x 9 9 0 1

Aplicando os intervalos, temos

V = 2 π 3 ∙ 1 - 4 ∙ 1 5 5 + 1 9 9 - 3 ∙ 0 - 4 ∙ 0 5 5 + 0 9 9

V = 2 π 3 - 4 5 + 1 9 - 0

V = 2 π [ 104 45 ]

V = 208 π 45

Prontinho!!

Resposta

V = 208 π 45

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queh) 0 ≤ y ≤ xex 2 + y 2 ≤ 2 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quef) 0 ≤ x ≤ 1ex ≤ y ≤ 3 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quej) 1 ≤ x 2 + y 2 ≤ 4ey ≥ 0 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quec) 1 ≤ x ≤ 4e0 ≤ y ≤ x
Considere um triângulo Isósceles situado no semiplano y ≥ 0 e com a base paralela ao eixo x. Mostre que o volume do sólido obtido pela rotação deste triângulo, em torno do eixo x, é igual ao produto d