Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 2

Determinar o volume do sólido de revolução gerado pela rotação, em torno do eixo dos x, da região R delimitada pelos gráficos das equações dadas.

y = x 2 + 1 ,   x = 0 ,   x = 2   e   y = 0

Passo 1

O gráfico que mostra a região R delimitada é dado por:

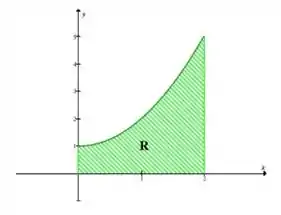
Passo 2

A equação do volume do sólido de revolução é:

V = π ∫ a b f x 2 d x

Substituindo pelos dados obtidos:

V = π ∫ 0 2 ( x 2 + 1 ) 2 d x = π ∫ 0 2 ( x 4 + 2 x 2 + 1 ) d x

Passo 3

Integrando:

V = π ⋅ x 5 5 + 2 x 3 3 + x

Aplicando os limites, temos:

V = π ⋅ 2 5 5 + 2 ⋅ 2 3 3 + 2 = π ⋅ 32 5 + 16 3 + 2 = π ⋅ 96 + 80 + 30 15 = 206 π 15

Resposta

206 π 15   u . v .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de O A .
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x + 1 ,y = 0 , x = 0 , x = 2 ;
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. x = 2 - y 2 , x = y 4 s o b r eoe
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = x 3 , y = 1 ,x =
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = e x ,y = 0 , x = - 1 , x = 1e