Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.2 - Ex. 14

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x .

y = sin ⁡ x ; y = cos ⁡ x

Passo 1

Bom galera, vamos começar encontrando x em que as duas funções se interceptam:

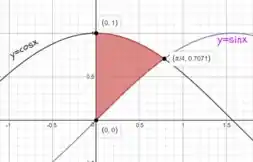
Logo, nossa integral vai de 0 até π 4 .

Passo 2

Belezinha, agora montamos nossa integral, lembrando que é um solido de revolução para a parte que fica entre a função e y = sin ⁡ x e y = cos ⁡ x :

V = π ∫ 0 π / 4 cos ⁡ x 2 - sin ⁡ x 2   d x

→ V = π ∫ 0 π 4 cos 2 ⁡ x - sin 2 ⁡ x   d x

Passo 3

Por fim, a gente resolve essa integral:

V = π ∫ 0 π 4 cos 2 ⁡ x - sin 2 ⁡ x   d x

Vamos usar a sugestão do problema, uma identidade trigonômetrica:

cos ⁡ 2 x = cos 2 ⁡ x - sin 2 ⁡ x

Logo nossa integral fica:

V = π ∫ 0 π 4 cos ⁡ 2 x   d x

= π sin ⁡ 2 x 2 0 π 4 = 1 2 π

Resposta

1 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Nestes exercícios, suponha que um sólido S de volume V seja delimitado por dois planos paralelos perpendiculares ao eixo x
Suponha que f seja uma função contínua em [ a , b ] e seja R a região delimitada pela curva y = f ( x ) e a reta y = k de x = a até x = b . Usando o método dos discos, deduza e explique uma fórmula pa
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo y . y = ln ⁡ x ; x = 0 ; y = 0 ; y = 1
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo y . y = x 2 ; x = y 2
Encontre o volume do sólido que resulta quando a região do exercicio 35 gira em torno da reta y = 3 .