Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 22

A energia total E(t) da corda vibrante é dada em função do tempo por

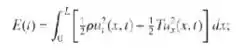
o primeiro termo é a energia cinética devida ao movimento da corda, e o segundo é a energia potencial criada pelo deslocamento da corda de sua posição de equilíbrio. Para o deslocamento u(x, t) dado pela Eq. (20) – ou seja, para a solução do problema da corda com velocidade inicial nula – mostre que

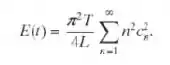
Note que a expressão à direita do sinal de igualdade na Eq. (ii) não depende de t. Logo, a energia total E é constante e, portanto, é conservada durante o movimento da corda..

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nessa questão, temos uma equação diferencial e precisamos aplicar os valores de contorno. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser determinar o formato da solução de função.

∂ u ∂ t =   - π a   ∑ c n n L sin ⁡ n π x L sin ⁡ n π a t L

∂ u ∂ x =   π   ∑ c n n L cos ⁡ n π x L cos ⁡ n π a t L

∂ u ∂ t 2 =   π ² a ²   ∑ c n n L 2 sin ² ⁡ n π x L sin ² ⁡ n π a t L + π ² a ²   ∑ F n m ( x , t )

∂ u ∂ x 2 =   π ²   ∑ c n n L 2 cos ² ⁡ n π x L cos ² ⁡ n π a t L + π ²   ∑ G n m ( x , t )

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

a ² = T ρ

E t = ∫ 1 2 ρ ∂ u ∂ t 2 + 1 2 T   ∂ u ∂ x 2 d x

E t = π 2 T 4 L ∑ n 2 c n 2

Resposta

E t = π 2 T 4 L ∑ n 2 c n 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a corda no Problema 10 começa a partir da posição inicial f ( x ) = 8 x ( L - x 2 ) / L 3 . Siga as instruções no Problema 10 para esse novo problema.
Se uma corda elástica tiver uma extremidade solta, a condição de contorno a ser satisfeita aí será u x = 0 . Encontre o deslocamento u(x, t) de uma corda elástica de comprimento L, fixa em x = 0 e sol
Faça o gráfico de ϕ ( x - a t ) para t = 0, 1/a, 2/a e t 0 / a se ϕ ( s ) = s e ns . Note que, para qualquer t ≠ 0 , o gráfico de y = ϕ ( x - a t ) é igual ao de y = ϕ ( x ) quando t = 0, só que deslo
Mostre que a equação de onda a 2 u x x = u t t pode ser reduzida à forma u x h = 0 pela mudança de variáveis ζ = x - a t ,η = x + a t Mostre que u(x, t) pode ser escrita como u ( x , t ) = ϕ ( x - a t
Considere uma corda elástica de comprimento L cujas extremidades são mantidas fixas. A corda écolocada em movimento a partir da sua posição de equilíbrio, com velocidade inicial ut(x, 0) = g(x). Em ca